
通过应用著名的埃伦费斯特定理,我们得到了在周期势能场中传播的电子的有效质量,该质量描绘了金属或半导体中原子核/离子的分布。
金属(或半导体)中电子的有效质量是一个从现象学上很有趣但在计算上却是近似的物理量。著名的埃伦费斯特定理(Ehrenfest Theorem)将在我们的论证中扮演关键角色,该定理由Paul Ehrenfest (图1)于1927年在波动力学中提出,可惜的是他于1933年自杀。具有讽刺意味的是,著名的意大利物理学家Et-tore Majorana于1938年神秘失踪(他是自杀吗?),1933年他留在莱比锡,就读于Werner Heisenberg任教的物理研究所。Ehrenfest的悲惨死亡在当时的科学界引起了强烈反响,正如Albert Einstein在他的回忆录中所述。相反,在我们所掌握的历史文献中,没有任何迹象表明Majorana有潜在的情绪反应。

图1:Paul Ehrenfest
埃伦费斯特定理表达了经典力学与量子力学之间的联系,尽管如上所述,它是在波动力学的形式中得到证明的。19世纪,英国数学物理学家L. Hamilton证明了粒子的运动等同于波的传播。Hamilton推导出了一个薛定谔型方程,其中出现了一个常数,其维度为作用量(能量×时间),并与著名的普朗克常数h等同(1900年)。当时没有实验证据支持这一结论,它仍然局限于纯数学形式。正是这种粒子-波等价性促使Erwin Schrodinger在1926年重新诠释了Hamilton发现的结果。
让我们参考前几期中介绍的一维toy model。如前所述,单电子态是布洛赫波或调幅平面波,其包络周期为a(晶格间距)。每个波都以波数k为特征,然而,波数k并不等同于粒子的动量,但仍是一个“好的量子数”。按照粒子的直观概念,单个电子可以用局域波来描述,即波包,在这种特定情况下,它不同于德布罗意波包,因为后者指的是自由粒子。因此,我们有一个布洛赫波包,其波函数如下:
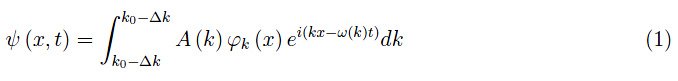
其中,φk(x)是周期调制包络,A(k)是包络中单个分量的振幅,并且假设在给定波数k0的邻域中达到极峰。函数ω(k)是上述分量的脉动(角频率)。这个量表达了色散定律,具有根本性的重要意义。事实上,对于自由粒子,φk(x)是常数,脉动由以下公式给出:

因此,德布罗意包以以下群速度传播:

其中p是粒子的动量,以波长表示为:p=h/λ。这里,λ被称为德布罗意波长。在toy model中,单个电子受到原子核产生的周期性势能V(x)的影响。因此,在积分(1)中,色散定律ω(k)不再由(2)给出,而是更加复杂,其解析表达式取决于V(x)的解析表达式。然而,很容易证明ω(k)是周期为2π/a的周期3。对于Max Born统计解释,复函数(1)的平方模数是在以上述函数计算点为中心的x轴无穷小区间内找到电子的概率密度。简单点说,我们可以说ψ(x,t)是电子存在的一种指标。根据概率定义:

这就是在典型的量子力学问题中会遇到波包的原因:积分的收敛由振幅A(k)的快速衰减保证(想象一个以k0为中心的高斯分布)。否则,电子向无穷远处移动的概率不为零(散射过程)。从统计解释来看,电子位置的平均值由波包(1)表示,即:

由此可知⟨x⟩依赖于时间t。利用这些要素,我们可以提出埃伦费斯特定理:

其中,me为电子的质量,V′(x)为V(x)的一阶导数。根据平均值:
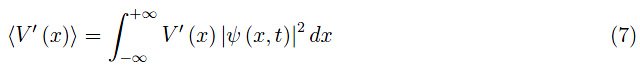
这里,⟨V′(x)⟩取决于时间。该定理的物理内容在以下情况下很有趣:

从方程(7)中我们可以看出,从数学上讲,如果V′(x)缓慢变化到|ψ(x,t)|2,就会发生这种情况,因此可以从积分中剔除,积分在该位置变为1。从物理上讲,如果V′(x)(也就是因此作用在电子上的力)在电子横坐标发生德布罗意波长量级的变化时可以忽略不计,则方程(8)成立。在这种情况下,方程(6)重现了应用于电子的牛顿第二定律:

因此,d⟨x⟩/dt与电子的经典速度一致。只要知道调制包络ϕk(x)和色散定律ω(k)(函数A(k)通过高斯分布或洛伦兹分布以现象学方式指定),就可以从(1)-(5)开始计算此量。但是,计算(1)中第二项的积分是不切实际的。另一方面,波包(1)以群速度vg=ω′(k)传播,其中顶点表示对k的导数,vg是最接近d⟨x⟩/dt的物理量。因此:

如上所述,波数k与动量p并不相同,但仍可近似为:

而dp/dt是作用于电子的力,即−V′(x),因此可得:
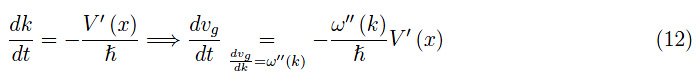
将其代入(10)中,并考虑方程(9),变为:

方程(13)是不合理的,因为除非我们考虑德布罗意包的色散定律,否则第二项并不与电子的质量重合,而德布罗意包的色散定律描述的是自由电子。在这种情况下,ω(k)由(2)给出,其中m=me.。因此,方程(13)简化为恒等式me = me.。如前所述,对于布洛赫波包,ω(k)是周期的(并且有界),因此它不能是k的二次函数。这决定了方程(13)的第一项对k的依赖性。可以通过将me重新定义为m*e(称为电子的有效质量)来克服这个结果的不合理性:

请注意,当ω′′(k)<0时,m*e (k)<0,且|m*e (k)|在色散曲线的拐点处→+∞。me(k)这个量得到了大量实验的证实,在三维推广中,它取决于波矢k的笛卡尔分量。
我们可以将方程(14)应用于我们的一维toy model,记住该模型与周期势的特定形状无关,因此与调制包络无关。对于普朗克-爱因斯坦关系,我们可以立即找到色散定律:
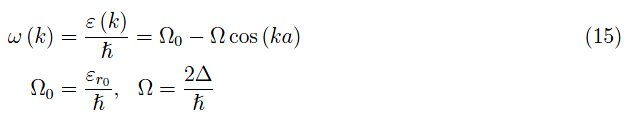
让我们快速回忆一下,起关键作用的是量(具有能量的量纲)∆>0,它衡量了单个胞极限下势能垒的降低。在(15)中,我们用Ω表示这个量,其量纲为角频率。项εr0是当∆=0(绝缘体的情况)时单个电子束缚态的能量。通过计算函数(15)的二阶导数,我们得到了toy model中单个电子的有效质量:

相应图表绘制于图2。
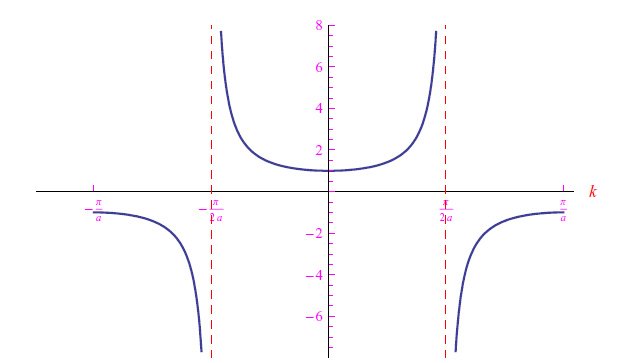
图2:toy model单个电子的有效质量,以无量纲单位表示
最后,我们通过向读者展示当∆=0时群速度始终为零来结束本篇文章。从物理上讲,这意味着单个布洛赫包是驻波的叠加。这个结果是正确的,因为∆=0在数学上表达了绝缘体的行为。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Effective mass – The Ehrenfest Theorem,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯