本文将提出一个基于回旋共振的实验来测量半导体中电子和空穴的有效质量。
在之前的文章中，我们通过霍尔效应测定了电子和空穴的迁移率，该效应需要将半导体置于均匀的静磁场中。为了测量电荷载流子的有效质量，除了静磁场外，我们还通过应用射频电磁场对这一技术进行了扩展。
为了使实验具有可操作性，有必要对带电粒子(电子或空穴)在均匀静磁场中的行为进行分析研究。由于涉及“微观”量，因此最好使用高斯系统作为测量单位，而不是国际单位(或MKS单位)。提示一下，下表很有用：
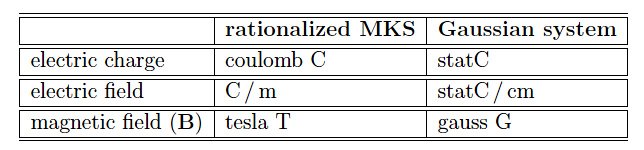
让我们记住1T=1Wb/m，以及1T=104G。
在霍尔效应的研究中，我们发现磁场通过洛伦兹力改变电荷载流子的轨迹，在高斯系统中洛伦兹力由下式给出：
其中：v为粒子速度，c为真空中的光速，q为电荷，B0为均匀静磁场。在不失一般性的前提下，我们以电子为例，因此q=−e。
在经典电动力学中，确定受洛伦兹力作用的带电粒子的轨迹问题的解决方案是众所周知的。然而，我们还是遵循了特定的步骤，这倒并不奇怪，因为我们仍然需要对牛顿第二定律产生的微分方程进行积分。简而言之，任何电动力学问题都可以归结为动力学问题。具体来说，我们考虑的是非相对论运动，即v≪c，因为是半导体物理学中的应用，其中电荷以低于光速的速度移动。
符号的问题，严格来说，应该从量子力学的角度来处理。
回到方程(1)，我们选择的参考系(Oxyz)的原点位于电子的初始位置，z轴方向与B0同步。从方程(1)中我们可以看出，如果电子最初处于静止状态，它将保持这种机械运动状态。为了对运动微分方程进行积分，我们使用了数学分析中常见的方法，然后通过软件(Mathematica)对获得的结果进行了比较。轨迹是一个圆柱形螺旋线，其轴线是一条平行于B0的直线，因此也平行于z轴，底部是一个半径为R的圆，该圆半径取决于初速度沿x轴和y轴的分量，以及一个具有角频率量纲的量ω(图1)：
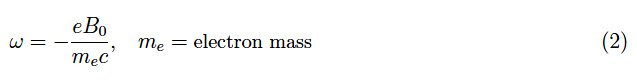
更确切地说，半径R取决于|ω|，即运动在坐标平面xy上的投影沿半径R的圆周行进的角速度的绝对值。我们称ωc=|ω|为电子回旋频率，而R被称为回旋半径(Larmor半径)。结果很直观：电子轨迹“包裹”着磁场B0的方向线，在带正电荷的情况下，轨迹不变，改变的是包裹的方向。
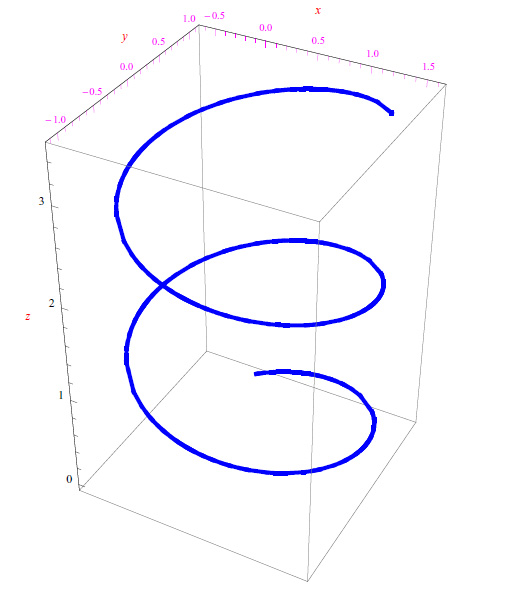
图1：软件重建的电子在均匀磁场中的轨迹。用笛卡尔轴上的坐标值表示
所有这些都是针对孤立电子而言的。对于半导体导带中的电子，由于与晶格势能的相互作用，问题会变得更加复杂。但我们已经学会了利用有效质量的技巧来绕过这个棘手的问题，这样回旋频率就变成了(符号的含义很明显)：
类似地，价带空穴的回旋频率也是这样定义的。如果对于给定的磁场B0，我们可以测量回旋频率，那么根据公式(3)我们就可以确定有效质量。
实验的初始配置是将半导体晶体置于均匀的磁静电场B0中。然后发送一个平坦的单频电磁波，该电磁波为圆极化，传播矢量与磁场平行且一致。晶体对电磁场的吸收率A，随着波的频率ω会发生变化。吸收曲线如图2所示，是共振过程的典型表现。换句话说，吸收峰出现在ω=ωc时，因此得名回旋共振(Cyclotron resonance)。
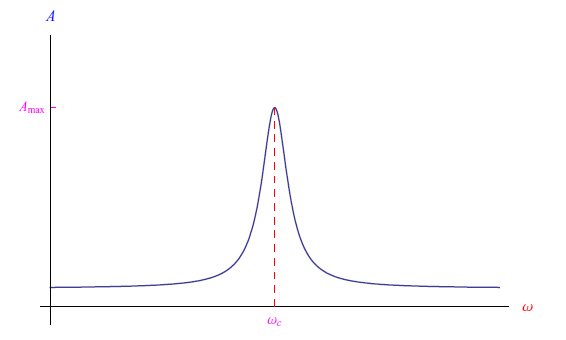图2：入射到半导体晶体上的电磁场的典型吸收曲线
让我们来研究一下吸收峰宽度γ的物理意义。在之前的文章中我们已经看到，在Drude-Lorentz模型中，金属传导电子(或半导体导带中的电子)的运动是由与晶格(或杂质)的一系列随机非弹性碰撞组成的，平均频率等于1/τr，其中τr是弛豫时间(在室温下约为10-14秒)。
另一方面，我们在上一节中指出，在存在磁场B0的情况下，单个电子的轨迹会环绕磁场，将其自身投影到垂直于磁场的平面上，相应投影的圆周运动角速度为ωc，这恰好是回旋频率。在前面提到的Drude-Lorentz模型中，我们必须考虑与晶格的碰撞，从而引入一个新的弛豫时间τγ，但它与无磁场时的弛豫时间τr成正比。由于吸收峰的宽度γ具有频率的量纲，我们预计它的倒数γ−1恰好为τ。这个结论通过以下运算在数学上得到证实：
这是两种在物理现实中不会发生的极端情况。但是，结论是正确的，这意味着我们的解释是正确的。简而言之，增加碰撞频率，曲线变宽，测量吸收峰和回旋频率会变得更加困难。因此，要想很好地测量ωc，需要非常纯净的半导体晶体，而且电子/空穴的浓度不能过高(降低与晶格碰撞的概率，从而降低碰撞频率)。
这可以通过将半导体的温度调至相对室温较低的水平来实现。此外，为了更加定量，实验成功的一个必要条件是γ−1>2π/ω，其中第二项是电子轨迹在垂直于磁场的平面上投影的圆周旋转周期。事实上，如果上述不等式得到验证，电子在经历新的碰撞之前就能完成一次完整的环绕。
至于ωc的数值，它通常在无线电波或微波的范围内，因此在后一种情况下，半导体被浸没在低温谐振腔中。磁场的量级为104G。
有科学文献报道了此类实验，其结果有力地证实了基于埃伦费斯特定理(Ehrenfest theorem)的模型的有效性。
(原文刊登于EDN姊妹网站Power Electronics News，参考链接：Scientific Notes on Power Electronics: Measuring the Effective Mass with Cyclotron Resonance，由Ricardo Xie编译。)
最前沿的电子设计资讯
