SDE是“随机微分方程”的缩写，是一种适用于电力电子领域的框架，特别是噪声的仿真和分析。在本文中，我们将把这一范例应用于Mathematica计算环境，来研究一些简单电路，当然该方法也可以推广到更复杂的电路。
在过去的几十年中，符号/数值计算软件(Mathematica、Maple等)的迅速普及，加上人工智能的最新发展，为在新的计算平台上仿真和研究复杂系统的行为提供了可能。具体做法是从物理现实中抽象出“因果”关系，然后通过“输入-输出”类型的计算模型对其进行描述。在具体情况的电气和电子电路下，这就产生了面向抽象的系统的概念，如图1中的框图所示。
图1：面向抽象的系统：一个输入vin对应一个输出vout
所考虑过程的确定性保证了输入→输出的唯一对应关系。然而，不可避免的随机过程(如噪声)的存在破坏了这种可能性，因此使用SDE框架是唯一可行的方法。
在线性系统中，瞬态阶段可以用一个确定所研究过程时间尺度的量来描述，这个量也就是时间常数。要从物理上解释这个量，最好先对一个恒定输入(图2)进行研究。为此，我们先看一个非常简单的电路：低通滤波器(RC系列)，然后使用Mathematica设置一个求解程序。
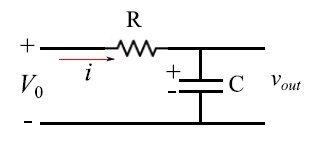
图2：RC系列受到恒定电位差的影响
假设电路在t=0时刻闭合，则根据基尔霍夫第二定律得出：
其中，vR=Ri是电阻两端的电压降，vout是电容器极板之间的电位差。如果q是极板上的电荷，则有vout=q/C，因此方程(1)变为：
根据i=dq/dt，我们有：
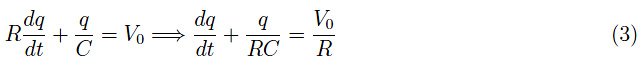
这是未知函数q(t)的一阶微分方程。它的特定积分由初始条件q(0)=q0唯一确定。后者是电容器板上的初始电荷。在不失一般性的前提下，我们假设电容器最初不带电：q(0)=0。
利用已知方法求解方程(3)，得到指数上升函数：
其中τ=RC是时间常数。从公式(4)我们可以看出，这个量决定了电容器充电过程的时间尺度：当t≫τ时，电荷实际上已达到稳定状态值CV0。此时，电流可通过导出函数q(t)来计算。
在图3中，记录了一个物理上很有趣的量的典型趋势。
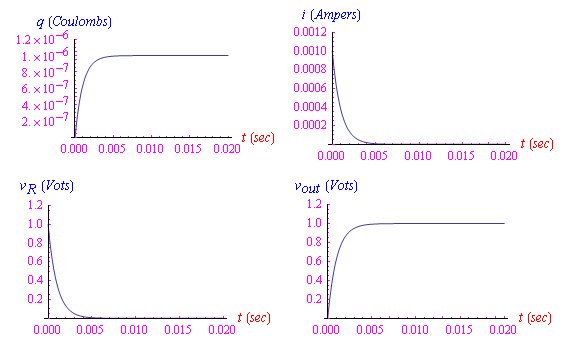图3：R和C取适当值，RC串联电路承受1伏特的电位差，当t≫τ时，系统稳定在固定值上。注意输出信号的指数上升
在vin(t)变量条件下，通过重复恒定输入的操作步骤，可获得电流、输出电压和R两端压降的变化趋势，然后再加上电阻耗散功率和电容功率的变化趋势(图4)。所用数据包括：R=1kΩ、C=1µF、VM=1V、f=50Hz。
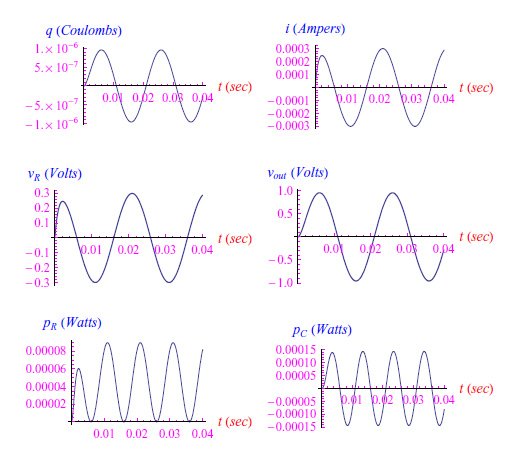
图4：RC系列受到正弦电位差的影响。请注意，初始瞬态受时间常数τ=RC的控制
当电阻R较小时，结果再现了电流相位比电压提前π/2的现象，如图5所示，其中我们使用了以下值：VM=1V、R=10−3Ω、C=10−3F、f=50Hz。增加电阻值(R=10−1Ω)后，我们得到了图6中的变化趋势，从中我们可以看到相位延迟明显减少。事实上，当R≪1时，电路是纯电容性的，而当R≫1时，电路是纯电阻性的。
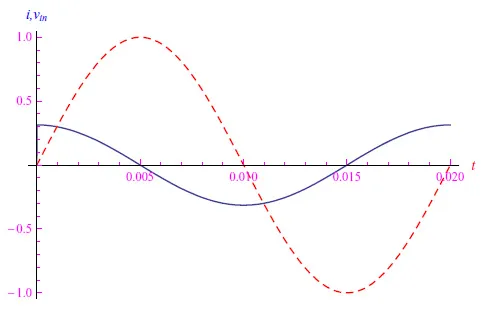
图5：RC系列，R可忽略不计。电流比电压vin提前约90°
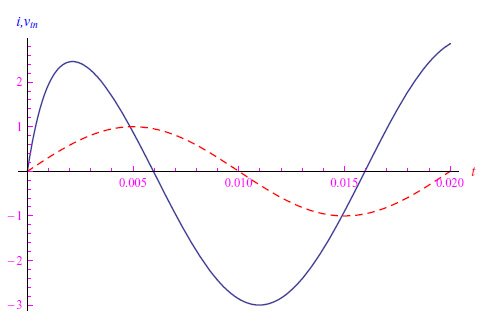
图6：RC系列，其中我们增加了R的值
输入信号中存在噪声，这破坏了使用以前的抽象系统表示方法的可能性，如图所示，该系统对因果相关性进行了建模。从形式上看，我们仍然可以写出微分方程，其中vin(t)是浸没在噪声中的确定性信号。这样，我们就有了一个SDE，不过它的分析研究超出了本文的讨论范围，而Wolfram语言可以让我们非常轻松地解决这个问题。例如，我们知道白噪声是一个100%不相关的随机过程，这意味着，即使我们知道这样一个随机变量在时刻t的值，我们也无法确定该变量在紧接着的瞬间的值。换句话说，完全没有相关性会时时刻刻破坏变量的连续性。
从数学分析的角度来看，白噪声是一种时间函数，在每个瞬间都呈现有限的不连续性(也称为“第一类”)，因此它会瞬间且不可预测地从一个值变为另一个值。这样的函数无法用解析方式表示，但是，使用Mathematica，我们可以生成一个随机值数组(遵循高斯统计)，其插值在各个方面都会返回一个函数，可用作给定微分方程的系数和/或已知项。随后在适当的初始条件下进行数值积分就可解决所提出的问题。值得注意的是，Wolfram语言是一种解释型语言，给定的输入单元与输出单元一一对应，与图1中的抽象导向系统如出一辙，如图7所示。
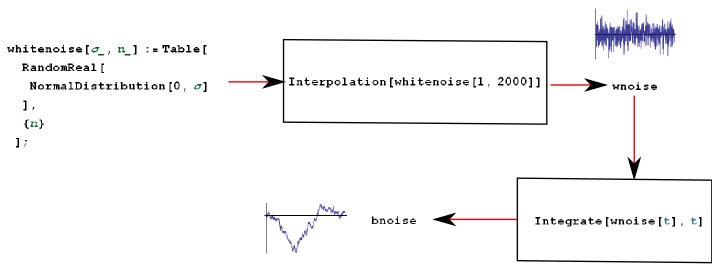图7：使用Wolfram语言生成白噪声和棕色噪声的过程框图
使用恰当的例程，我们就获得了图8中的变化趋势。
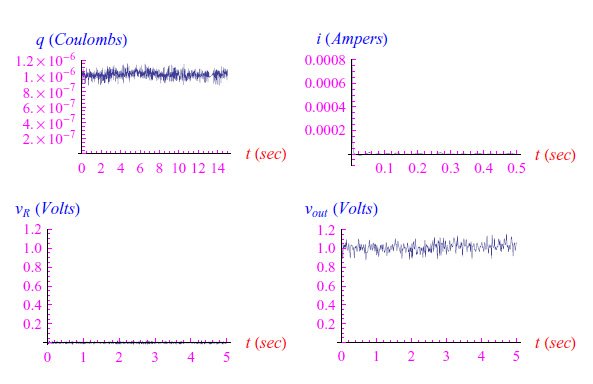图8：RC系列的输入由一个恒定信号和白噪声与棕色噪声叠加组成
Wolfram语言的研究引发了一些有趣的思考。首先，我们意识到数学实体与该编程语言(其结构让人想起Pascal编程语言)实现的对象之间存在一一对应关系，例如，所谓的 “InterpolatingFunction对象”，它们又是一个纯函数。其次，是为生成随机变量而开发的程序。在最后一种情况下，一个算法或确定性过程被用于生成另一个本质上是非确定性的过程，这让我们反思，是否有可能像人类智能一样，通过复杂的算法来产生不可预测的行为。
(原文刊登于EDN姊妹网站Power Electronics News，参考链接：Scientific Notes on Power Electronics: SDE Framework in Electronics，由Ricardo Xie编译。)
最前沿的电子设计资讯
