利用Wolfram语言(Mathematica)的灵活性，您可以在软件中重建线性网络的行为。在本文中，我们将研究电子学中的两个基本电路：低通滤波器和高通滤波器，它们与输入信号无关。
在正弦状态下的线性网络中，使用符号法具有无可争议的优势，即可以绕过对微分方程进行积分的棘手问题，这些微分方程涉及电容器和电感器等无源元件引起的电流强度和电压降等量。然而，随着所谓的C.A.S. (计算机代数系统的缩写，如Mathematica、Maple、Maxima等)的广泛传播，这种方法已经过时，因为这种方法只能用于正弦状态，并且忽略了不可避免的初始瞬态。
有一本很棒的书介绍了Mathematica的Nodal包，不过这个包使用的是符号法，因此无法充分利用Mathematica软件的强大功能和灵活性。我们的想法是使用一种面向微分方程的方法，而Mathematica可以通过DSolve和NDSolve指令可以很好地处理微分方程：前者以封闭形式返回解，而后者则执行数值积分，在这种情况下不可能找到可以用解析方式表达的解，即便是通过数学物理的特殊函数也不行。
线性网络的基本元件是电感器和电容器，当然，电阻器也起着关键作用，但它们不会通过从电流到外加电压的转换来改变波形(记住欧姆定律)。对于电容为C的电容器，施加到极板上的电压v(t)决定了电荷q(t)=Cv(t)，因此电流强度为：
电压v随时间变化越快，电流强度就越大。在正弦状态下(或在任何可展开为串联/傅立叶积分的情况下)，随时间变化的速率越快，频率就越高，换句话说，电容器只“让”最高频率的电流通过(在电气工程手册中，这种通过的行为，用电容器在高频下是短路来表达)。从数学上讲，电容器由导数算子表示。
电感具有双重特性。自感系数为L的电感两端的电压降为：
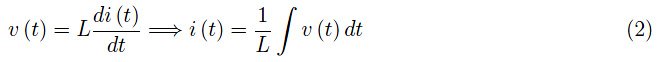
从数学上讲，电感用积分算子表示，而我们知道积分算子是导数算子的逆。从电路上看 ，电感在低频下表现得像短路。通过组装无源元件R、L和C，我们可以得到一个线性网络，该网络在数学上用微分或积分微分方程表示。图1所示的输入/输出系统就是一般线性网络的示意图。
图1：线性网络。输入信号vin唯一对应于输出信号vout
但即使从单个L或C元件开始，也有可能仿真出有趣的行为，如图2所示。
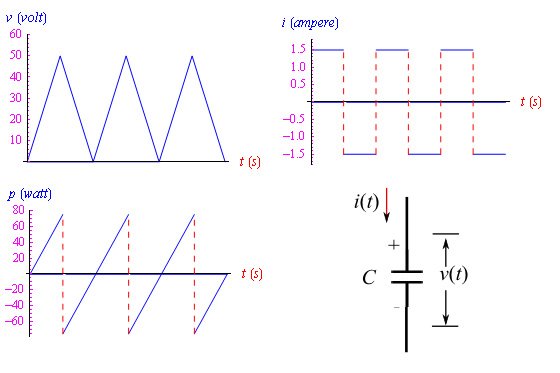图2：在电容为C的电容器上施加“三角波”类型的信号。其余图形分别表示电流强度和瞬时功率
在图3中，我们看到一个受白噪声影响的正弦信号，该信号应用于RC系列的输入。
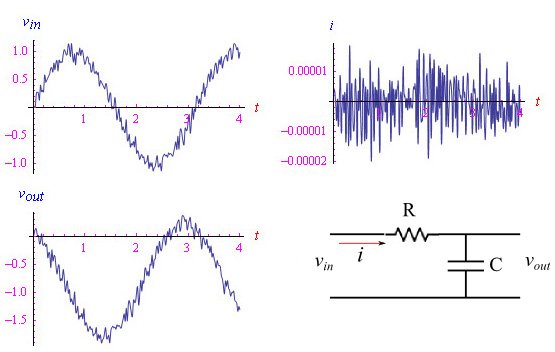图3：白噪声中的正弦信号
CR系列(图4)是高通滤波器，因为在高频下电容器是短路的。对于以串联方式产生的任何输入(如果是周期性的)或傅里叶积分，CR系列仅让高频电流通过。为了确定滤波器响应与频率的函数关系，可进行正弦测试输入vin(t)=VMsin(2πft)。更准确地说，通过使用Mathematica的DSolve指令求解相应的方程，我们得到输出信号vout(t)。
图4：CR系列
我们注意到，虽然符号法允许我们绘制相对振幅模块(out vs in)，表明CR系列是高通滤波器，但在我们的解决方案中，由于输入和输出之间的相位差由电容决定，因此无法实现这一点。但是，我们可以绘制频率f变化时的两个信号，如图5所示，其中我们使用了一个电阻器R=1kΩ和一个电容C=1µF的电容器。
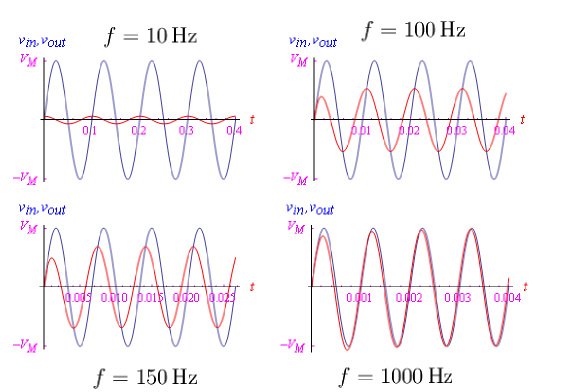图5：不同频率下输出信号与输入信号的比较。蓝色正弦波是输入信号，红色正弦波是输出信号。不仅要注意低频的衰减，还要注意两个信号之间的相位差
对于RC系列(图6)，微分方程的解仍然是Mathematica在高通滤波器中找到的解，因为我们所做的只是交换了元件。由于vout=vC，所以输出信号发生了变化，因此：
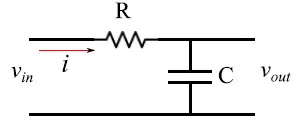
图6：RC系列
重复高通滤波器情况下的操作步骤，我们得到图7所示的图，其中R和C的值保持不变。
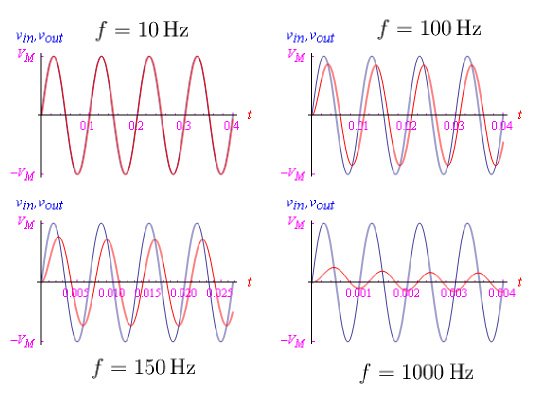图7：不同频率下输出信号与输入信号的比较。蓝色正弦波是输入信号，红色正弦波是输出信号。请注意高频下的衰减
最后，我们用一个高通滤波器结束本文，该滤波器的输入信号是高斯调制的正弦振荡。在这种情况下，Mathematica无法解析积分微分方程，因此我们使用NDSolve指令，假设振荡频率f为自由参数，观察信号是否具有周期性。图8显示了R=1kΩ和C=1µF时的结果。
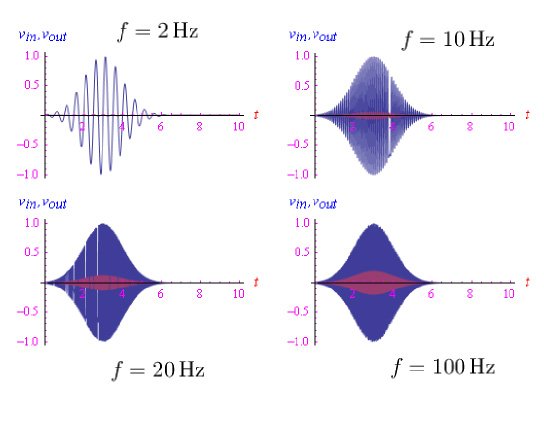图8：不同频率f下幅度调制正弦振荡的输出信号与输入信号的比较。蓝色图为输入信号，红色图为输出信号。注意低频处的衰减
(原文刊登于EDN姊妹网站Power Electronics News，参考链接：Scientific Notes on Power Electronics: Linear Networks and Wolfram Language，由Ricardo Xie编译。)
最前沿的电子设计资讯
