
在带有无源和电抗元件的电子电路中,即使信号瞬时变化(例如方波),电荷也会继续保持连续,我们将用一个“积分电路”来演示这一论断。
我们正在处理一个复杂的问题,假设电荷q(t)是时间t的连续函数,这对于含有有源半导体元件的电子电路,尤其是基于碳化硅(SiC)和氮化镓(GaN)的器件来说,可能并不成立。事实上,在半导体中,由生成/复合过程引起的电荷瞬时变化是无法排除的,因为相应的特征时间在时间尺度上可能是瞬时的,而这个时间尺度通常由宏观量(欧姆电阻、电感、电容)确定的时间常数决定。
通常,人们倾向于将生成/复合过程的贡献与电荷密度分开,从而引入“生成/复合率”。但我们认为,这种表述是一种有用的数学技巧,没有先验的理由排除半导体电荷q(t)可能存在的有限不连续性,我们将在后续文章中探讨这个问题。
在之前的文章中,我们研究了一个简单的RC串联电路,在任何输入的情况下都会返回一个输出(在电容器两端),该输出通过“求积”进行数学计算,也就是通过积分计算。因此,在模拟电子时代,这类电路被称为(输入的)积分器,或者更准确地说,是半积分器,因为被积函数等于输入乘以一个指数,该指数代表电路的时间常数。
对于正弦曲线等非常规则的输入,通过求积计算过程没有问题,在Wolfram语言中,它允许您根据以下定义实现所谓的Wolfram机:
定义1:我们将Wolfram语言中的所有符号计算过程称为Wolfram机。
因此,Wolfram机(WM)是一种程序,与传统编程语言(Fortran、C++等)的程序不同,它允许将自由参数作为自变量处理。例如,在RC系列的情况下,自由参数是电阻R和电容C的值,也可以是输入信号的任何参数(例如,如果信号是周期性的,则为频率)以及其他物理量。
在Mathematica的前端,用户可以定义一个函数,该函数以上述参数作为参数,并用下划线标记(以实现模式)。该函数将调用DSolve指令,该指令本身也是一个函数,其参数是待求解的微分方程和初始条件(注意,在Mathematica中,每条指令都是一个函数)。
用户自定义函数的作用体现在它能够根据用户指定的参数值(例如电容器的电容值)确定输出。
回到正题,让我们来考虑一个积分电路,其输入信号会发生瞬时变化。最简单的情况就是周期为T的方波:
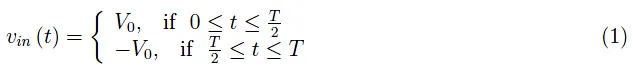
该输入触发了与表示基尔霍夫第二定律的微分方程有关的相应初值问题的“嵌套”结构:
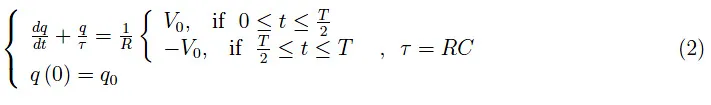
这就需要把周期区间[0,T]分解为两个不相交的子区间:
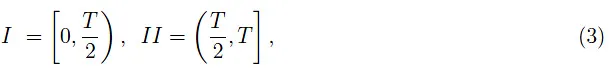
排除T/2中的不连续性,方波的情况可以很容易地用纸笔求解,然后用Mathematica绘制,找到电荷q(t)和电流强度i(t)的变化趋势(对于V0=1V,T=1s,R=1kΩ,C=10-4F),如图1所示。
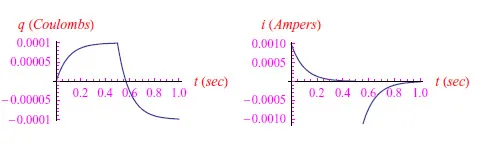
图1:方波的电荷趋势和一阶导数(电流)。注意q(t)图中有一个角点,它对应于电流i(t)的有限不连续性。
然而,我们感兴趣的是输出,即电容器两端的电位差vout=q/C,因此其趋势与电荷相同。图2中显示了R=1kΩ、C=10-4F时的输出趋势。通过增加电容器的电容(C=5×10-4F),我们获得了图3所示的趋势。
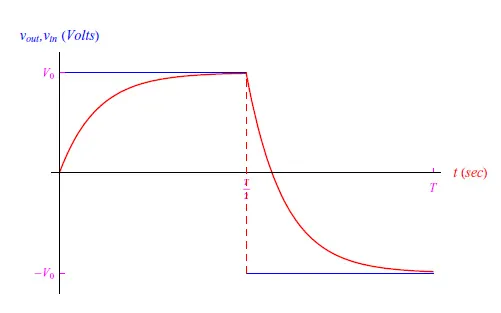
图2:输出信号趋势
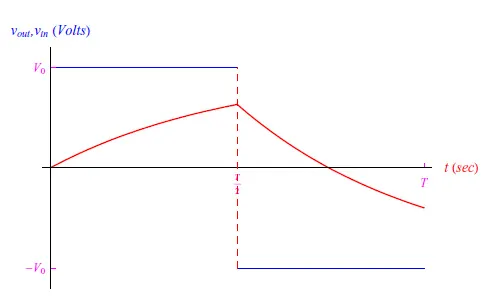
图3:增加电容器电容后输出信号的变化趋势
函数q(t)的连续性简单地表示了“电荷”这个物理量不允许不连续的情况。q(t)的导数,即电流强度i(t),可以具有有限的不连续性,因为电荷载流子的运动可以瞬间反转(随着电势差的反转)。
另一个例子是周期输入信号T=1s,它仍然可以用纸笔求解,但比较繁琐:
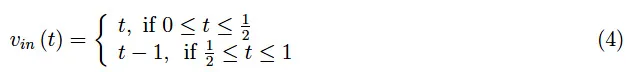
假设峰值为1V(图4)。这种类型的信号被称为锯齿波。在Mathematica中,周期区间[0,1]的分解由Piecewise指令完成。
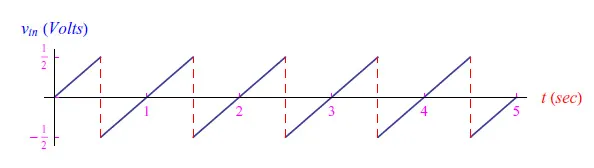
图4:锯齿波
重新组合用于方波的WM,我们获得了图5和图6中所示的电荷和电流强度趋势。
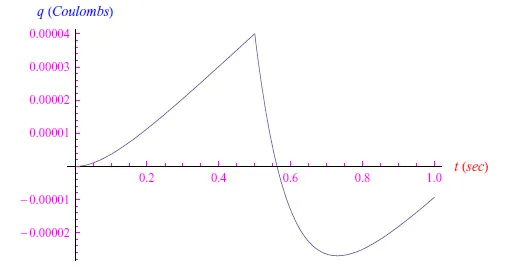
图5:锯齿波输入的电荷行为
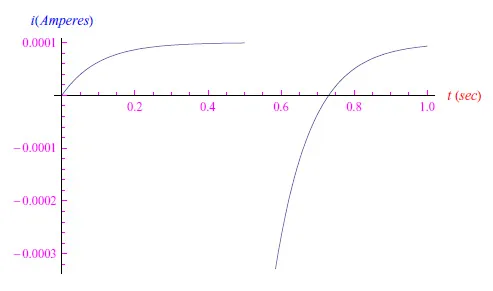
图6:锯齿波输入的电流强度趋势
然后,计算输出电压,我们就得到图7中的图表:R=1kΩ,C=1.5×10-5F。增加电容器的电容(C=1.5×10-4F),我们得到图8所示的图表。
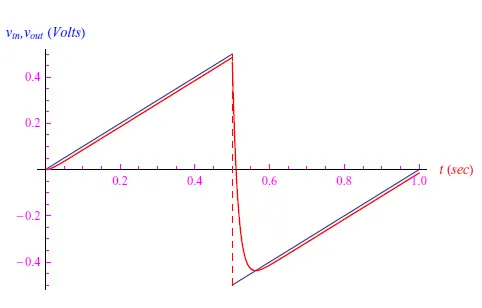
图7:输出电压与输入电压的比较。电容的低值再现了输入信号
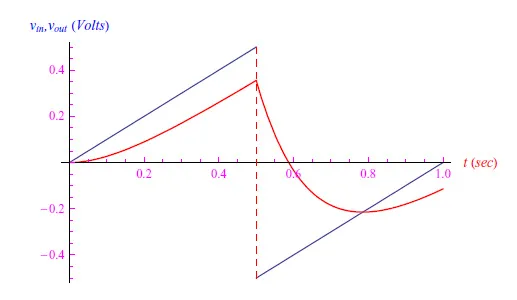
图8:输出电压与输入电压的比较,与上图中的值相比,电容器的电容有所增加
以下是一些建议的练习,我们将在下一期文章中给出答案。
练习1:RC积分电路的输入是:
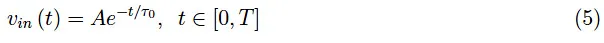
其中,A=10V,τ0=1s是特征时间(不要与时间常数τ=RC混淆),T=8s是周期。信号行为如图9所示。
对WM进行编程,使其能够针对R和C的值重建输出信号。
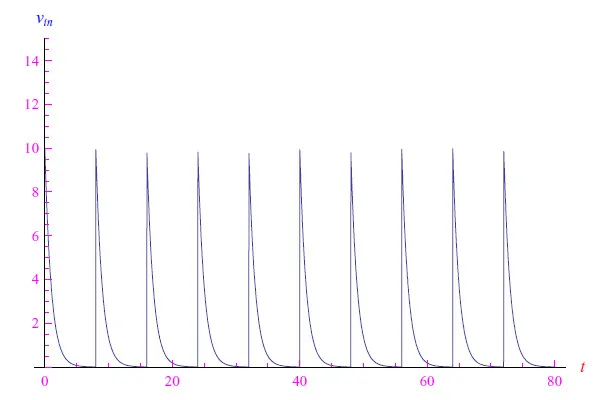
图9:信号趋势(公式(5))
练习2:1)解释为什么方波信号(1)的基尔霍夫微分方程无法积分。2)将方波(1)的傅里叶级数截断为给定阶数n后,确定输出信号,其中输入信号是傅里叶级数的n阶部分和。将电容接地是否可以减弱吉布斯现象的振荡?(请尽量定性回答)。
(原文刊登于EDN姊妹网站Power Electronics News,参考链接:Scientific Notes on Power Electronics: Integrator Circuit and Continuity of Electrical Charge,由Ricardo Xie编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯