在许多电子学书籍中，“单位脉冲”(或“狄拉克脉冲”)都是以公理形式呈现的，但这忽略了其物理意义，尤其是实际实现。在本文中，我们将通过虚拟实验来定义这一重要波形，以强调其在电路中的应用。
单位脉冲是由理论物理学家P.A.M. Dirac在20世纪20年代在其著作《量子力学原理》中通过所谓的狄拉克函数δ(x)引入的。该函数在除原点外的整个实轴上都为零，而在原点处趋向于+∞，由于不存在具有此性质的函数，δ(x)被称为非真函数。后来，这个概念通过分布的概念被公理化，但与此同时，许多数学家并不接受这种形式主义。
例如，著名数学家John Von Neumann在其名著《量子力学的数学基础》中写道：“Dirac的方法…完全不能满足数学严谨性的要求…例如，该方法遵循这样的假设：每个自伴算子都可以写成对角形式。而对于那些并非如此的算子，则需要引入具有自相矛盾性质的“非本征”函数。”
这里对狄拉克δ函数的看法显而易见。不过目前，狄拉克δ函数不仅用于量子力学，还用于电子学、电气工程和信号理论等许多其他领域。
让我们参考一个纯电阻电路，它受到持续时间为T0的矩形脉冲的影响(图1)：
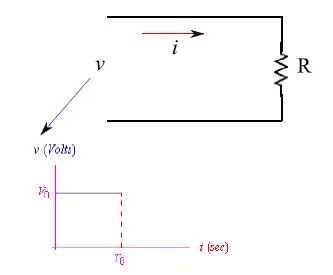
图1：纯电阻电路，其中输入电压由公式(1)给出
图2中绘制的电流由以下公式给出：
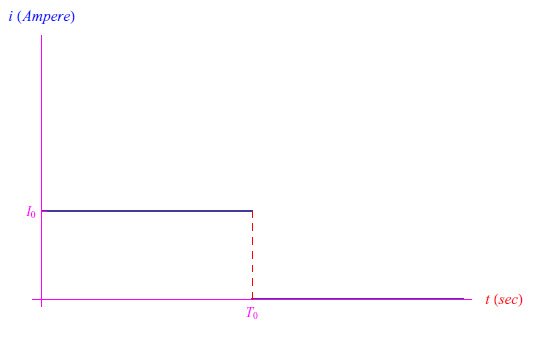图2：图1电路中的电流
图3中绘制的电荷由以下公式给出：
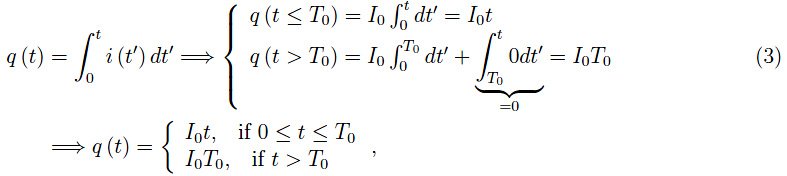
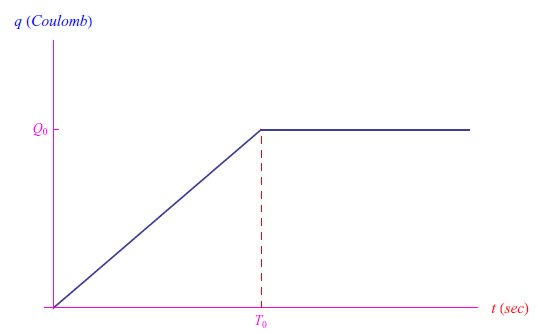
图3：公式(2)给出的电流对应的电荷
从几何学上讲，电荷的最大值(Q0)是边为T0和I0的矩形的面积：Q0=I0T0。
让我们重复实验，重新施加(1)式的矩形脉冲，但持续时间变为T<T0，幅度更大，以使电荷值Q0保持不变。如上所述，Q0是电流图矩形的面积，因此可以方便地根据i(t)进行推导。
矩形的面积相等：
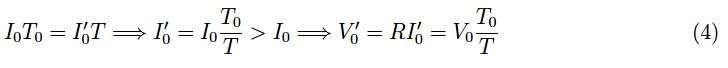
最后一个方程给出了矩形脉冲的新幅度。该过程可以不断迭代，或者更好的方法是，假设T<T0为独立变量，然后研究电路在T→0的极限下的行为。由于我们希望最大电荷Q0的值保持恒定，因此，通过将各个量用Q0表示，可以方便地摆脱T0的限制。通过对符号进行重新定义，我们可以得到：
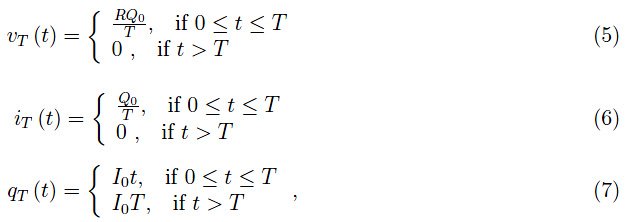
下标T提醒我们这个量是一个自由参数。图4中的图表总结了T0和T<T0时的趋势。
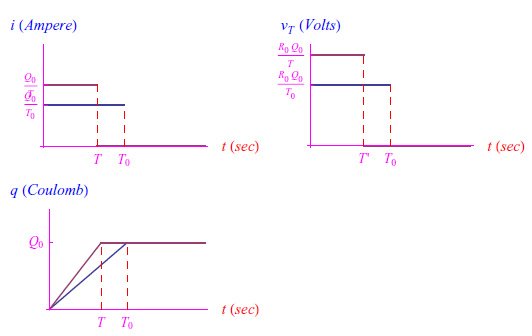
图4：公式(5)-(6)-(7)的趋势
根据公式(3)，我们得到：
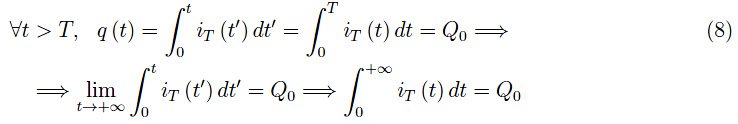
当T→0时会发生什么？为了找到答案，我们将极限算子应用于最后一个等式的第一个和第二个元素：
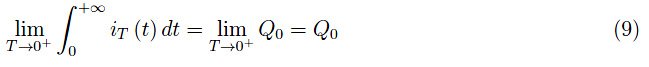
让我们尝试将极限算子放在积分符号下：
从方程(6)可知：
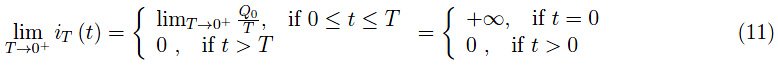
这又让我们回想起之前提到的狄拉克δ函数。更重要的是，积分(10)是有问题的，因为在积分的下界中，被积函数存在一种我们不知道如何处理的奇点。不过，我们很快就会看到如何摆脱它，我们假设方程(11)可以重写如下：
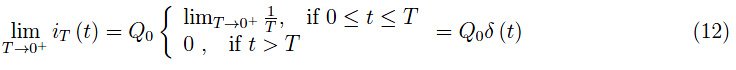
下列方程给出了狄拉克δ：
这个过程的结果在概念上很简单，因为如果我们不断减小脉冲的宽度，同时保持封闭面积恒定，那么在宽度无限小的极限内，振幅必然趋向于+∞，面积将以0-∞的不确定形式出现，这在任何情况下都必然会给出一个有限量(Q0)。
方程(10)变为：
摆脱积分下限奇点的一个巧妙方法是将后者移至−∞，然后通过对纵坐标轴对称的方式重新定义电压vT(t)，从而重新定义电流iT(t)：
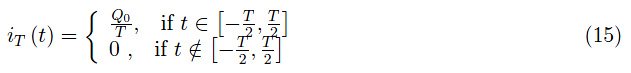
此外：
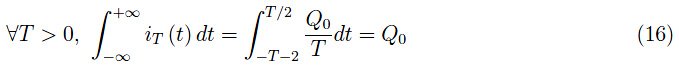
应用极限运算符：
这次将极限算子放到积分符号下就没有问题了，因为我们已经将积分的下限从0移到了−∞：
因此：
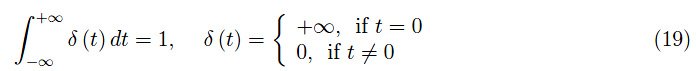
图5中显示了电流强度达到T→0时的极限运行情况。
图5：函数(15)在T→0+时的图形。脉冲所围成的矩形面积无论T是多少都是常数，等于电荷Q0
单位步长由下式给出：
它常常与Heaviside函数混淆，因为两者在t=0时都有有限的不连续性，不过与单位阶跃不同，后者在t=0时没有定义。
请注意，狄拉克δ是单位阶跃(也是Heaviside函数)的导数。在Mathematica中，狄拉克δ和单位阶跃是内置函数，可通过命令DiracDelta[]和UnitStep[]调用。
以下是一些建议的小练习，我们将在下一期文章中给出答案。
练习1：确定电阻在狄拉克脉冲作用下因焦耳效应而耗散的功率。
练习2：当输入信号是相对于二极管反向偏置的狄拉克脉冲时，研究包含二极管和串联电阻的电路的整流特性。
(原文刊登于EDN姊妹网站Power Electronics News，参考链接：Scientific Notes on Power Electronics: Unit Impulse and Unit Step，由Ricardo Xie编译。)
最前沿的电子设计资讯
