
系统效率对整体仿真的结果相当关键。图8,图9和图10体现了效率值和相关的损耗。如我们预想的,更高的输入电压会带来更高的整体效率,因为IPHASE降低(图8)。
对于不同电感带来的结果,可以看到更高的感值可能会带来更高的效率。然而,有许多其它的器件会影响结果。它展示了仿真带来的好处,因为效率计算和不同工作节点时器件考量是非常繁琐的。图10提供了绕组损耗的细节;不同感值带来的绕组损耗差异比系统损耗差异小。
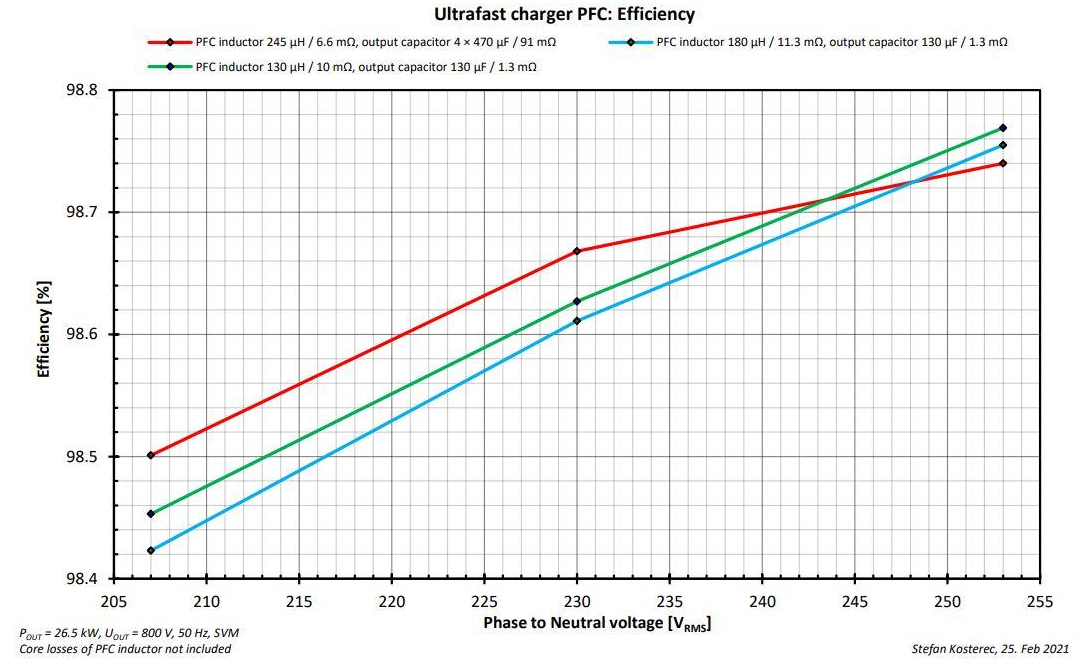
图8. PFC部分的效率和输入电压值、感值和输出容值的关系
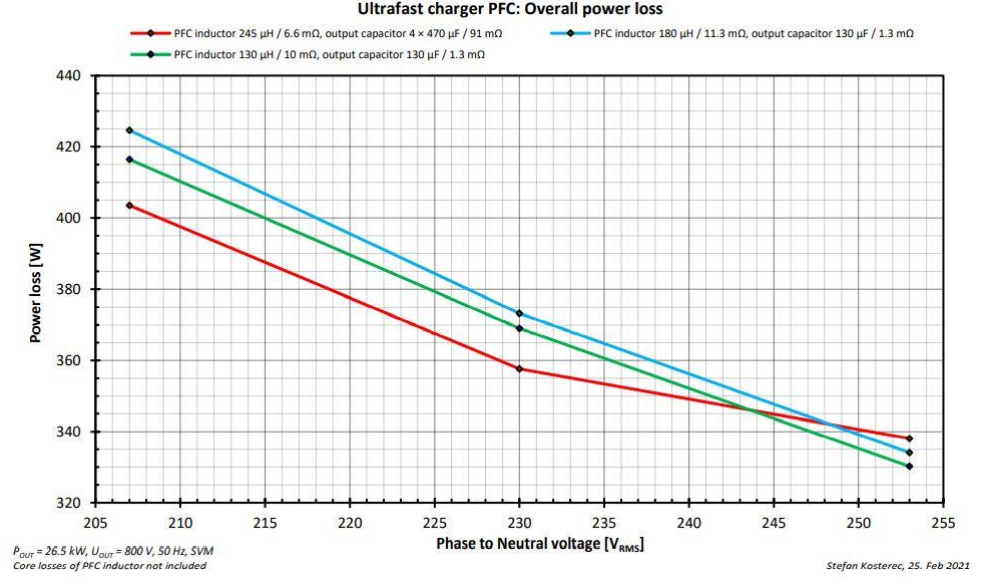
图9. PFC部分的损耗和输入电压值、感值和输出容值的关系
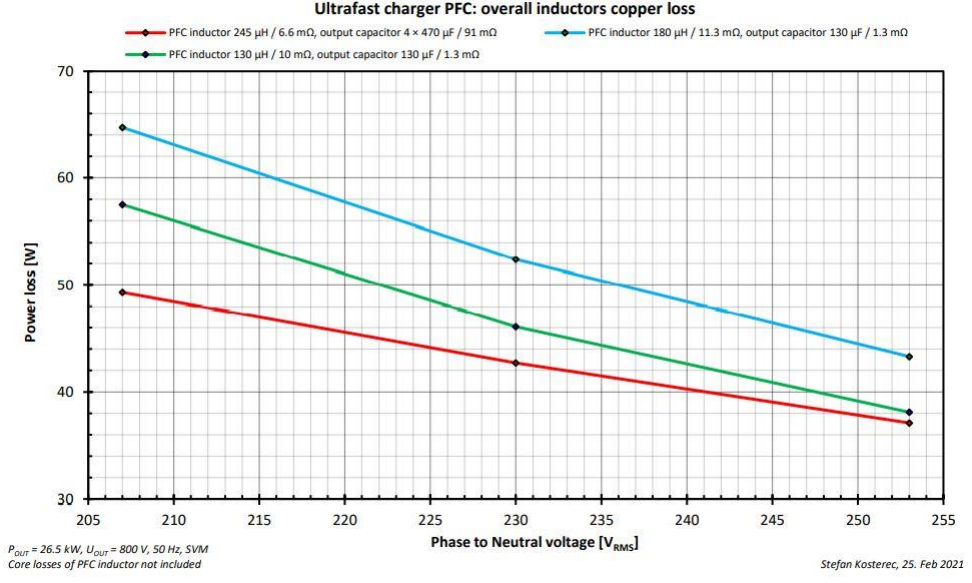
图10. PFC部分的电感损耗和输入电压值、感值和输出容值的关系
有关功率模块的损耗,仿真带来了有趣的信息(图11)。模块的损耗仅和感值相关。原因应该是更低的感值会带来更大的纹波电流,纹波电流越大,导通电流越低,所以开关损耗也降低了。
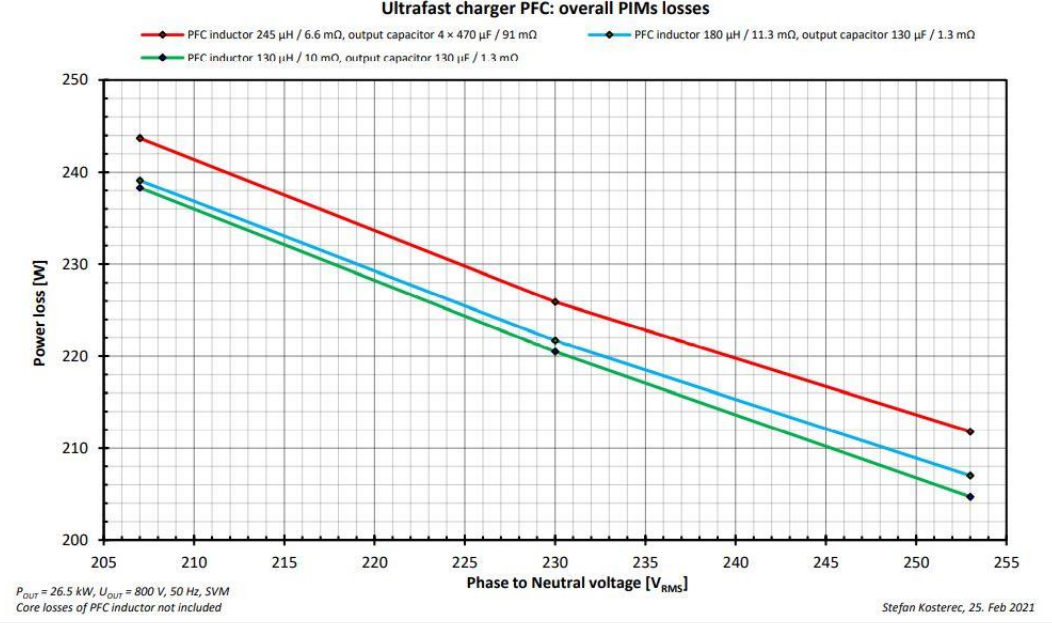
图11. PIM模块的整体损耗和输入电压值、感值和输出容值的关系
然而,功率模块和感值没有直接联系,因为调节的过程和PWM等也造成了影响。基于实际模型的仿真有助于预测结论即使无法直接确定实际关系。
最有趣的发现是模型中多个元素(器件)造成的损耗分布(图12)。这个分布图能够帮我们搞清楚损耗的来源以及哪些部分需要关注从而提高效率。本次设计中,我们证明了在各种情况下系统效率都会大于98%,所以有关效率,没有什么问题。有了这些结果,我们可以选择最能满足其余系统需求的解决方案。
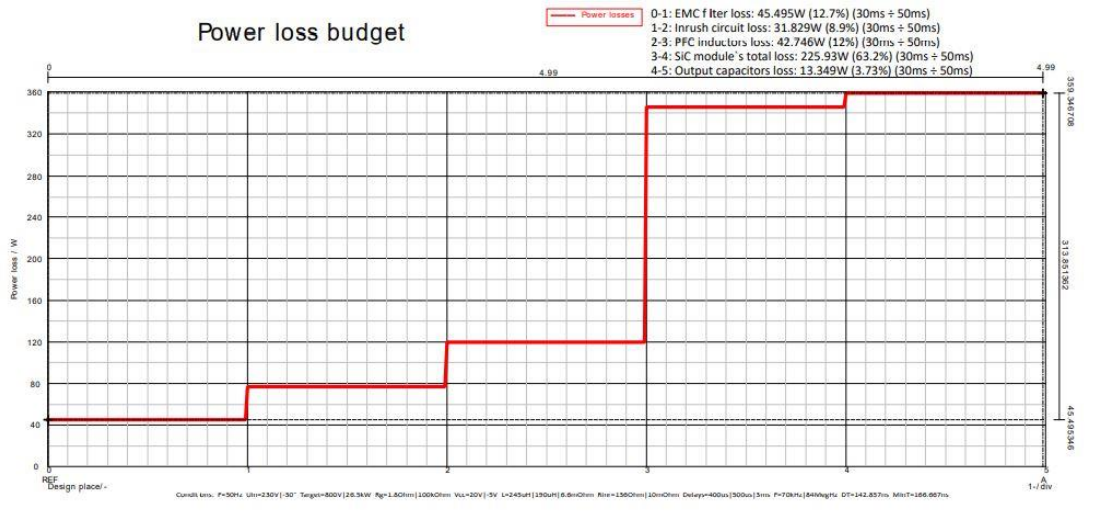
图12. 损耗的示意图。仿真的主要条件是VIN=230V,POUT=26.5kW,VOUT=800V,感值容值为245μH、4×470μF。仿真的时间为50ms。能量损耗计算时,时间设置基本考虑30ms至50ms (用“30ms % 50ms”表示),以保证系统运行在稳定阶段。
浪涌电流控制仿真的主要目的是为了确认尖峰和电流有效值,以及在启动时由限流电阻带来的损耗。这项仿真能够帮助我们去验证限流电阻的选型。
一般来说,启动时的峰值相电流(100μs以内)被限制在额定值的数倍。同样的,最大的相电流有效值也可以通过设置一个重复启动前的等待周期(几秒钟)来限制。
图13和图14展示了我们的系统在最差情况下的结果:母线相-零电压为310Vrms,A相从0点偏移了-30°,450μF的输出电容完全被耗尽。仿真告诉我们重复启动应该设置一个4.19秒的冷却时间以确保7W的损耗要求(抗浪涌电阻的功耗)。然而,一般来说充电系统不会在短时间内重复启动(几秒内)。
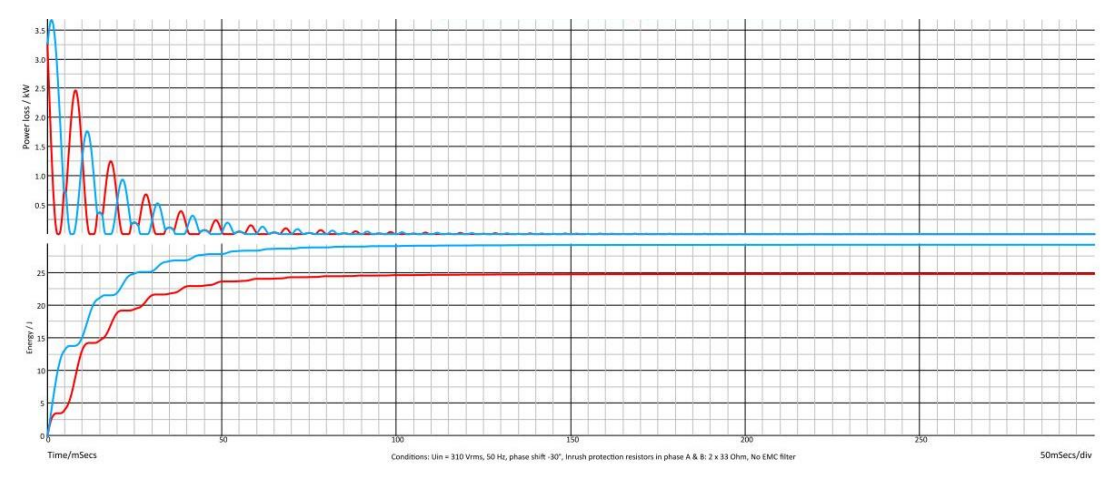
图13. 浪涌电流保护。最差情况下,启动时功率损耗(顶部)和能量耗散(底部)波形,浪涌保护时COUT=450μF,VIN=310Vac。浪涌保护由每相2个33Ω电阻串联组成(共4个电阻)。红线:一颗抗浪涌电阻功率和能量(A相)。蓝线:一颗抗浪涌电阻功率和能量(B相)。A相和B相分别由24.81J和29.29J能量耗散,7W的功耗限制下的冷却时间分别是3.55秒和4.19秒。
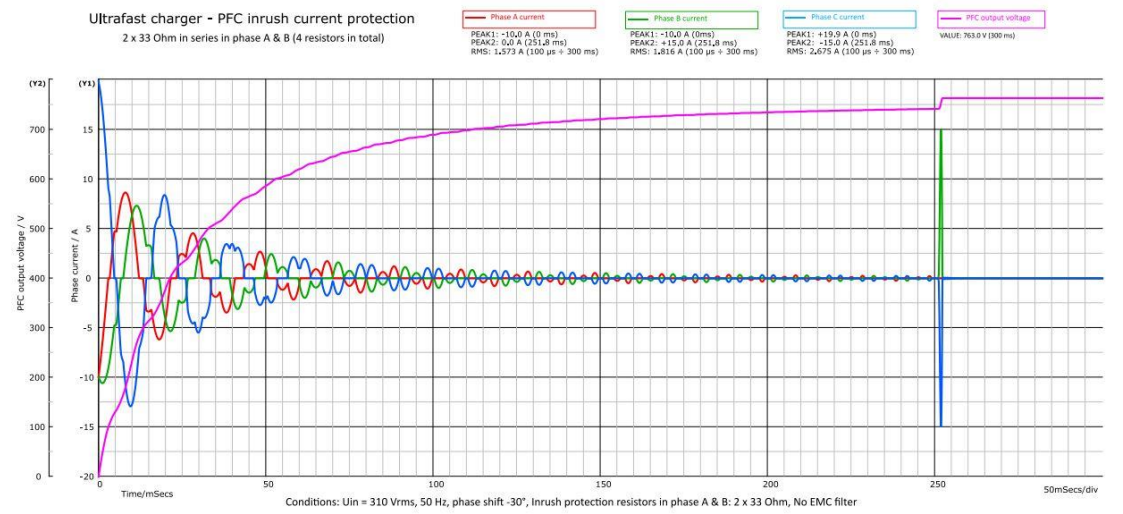
图14. 浪涌电流保护。浪涌电流保护时A相和B相的输入电流以及PFC输出电压。与图13一样,与保护电流和COUT有关。
功率因数是一个关键的要求,EV快充规定要求功率因数满载下必须达到0.99。图15验证了所有设计都能满足功率因数要求,图16呈现了一个完美的正弦电流波形以及IPHASE-VINPHASE关系。
无论感值如何变化,IPHASE,RMS几乎保持不变(图17),与总体效率结果相吻合(图8),因为不同型号的电感之间的变化也非常小。在峰值电流上可以观察到稍大的变化(图18),但IPHASE,PEAK值对功率损失并不关键,因为IPHASE,RMS才是用于估计损失和效率的主要因素。
可以确定地是电流越大,系统损耗越大。总谐波失真(THD)结果也体现了这一点(图19)。
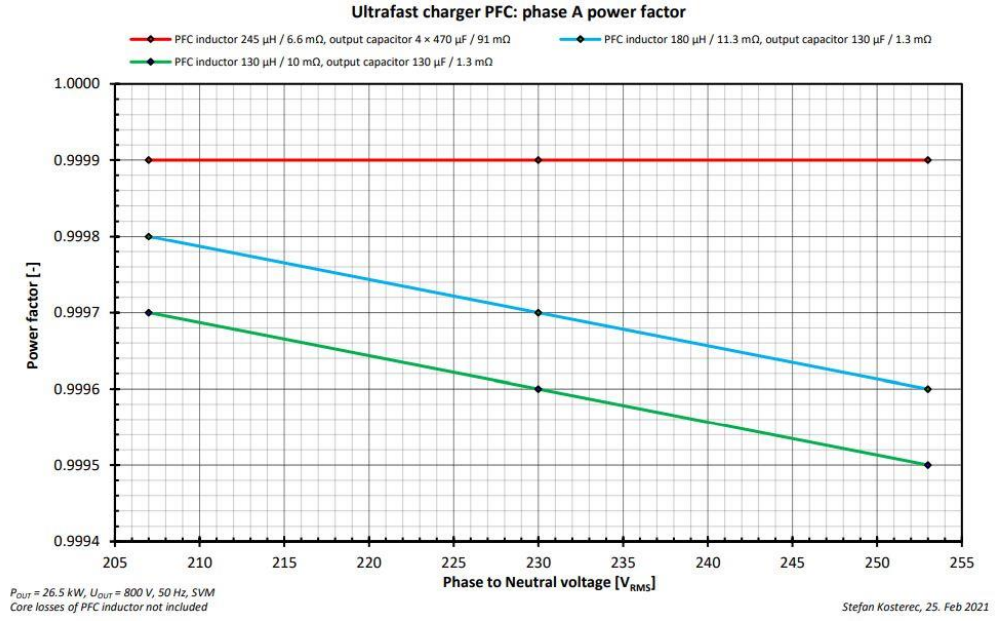
图15. 功率因数和输入电压值、感值和输出容值的关系。所有情况的功率因数均>0.99。
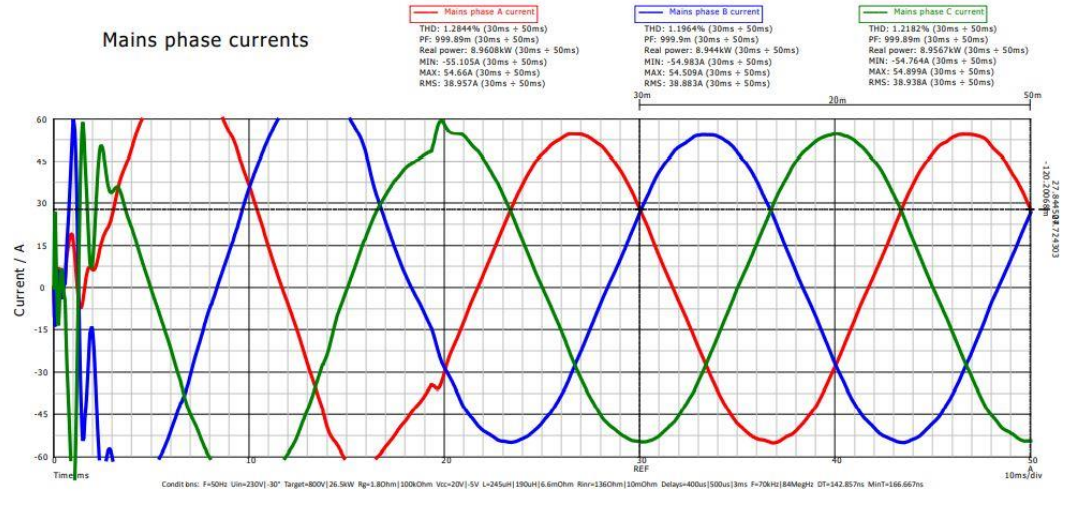
图16. 相电流曲线,PFC电感245μH。PFC A相功率因数0.999,VIN=230V。
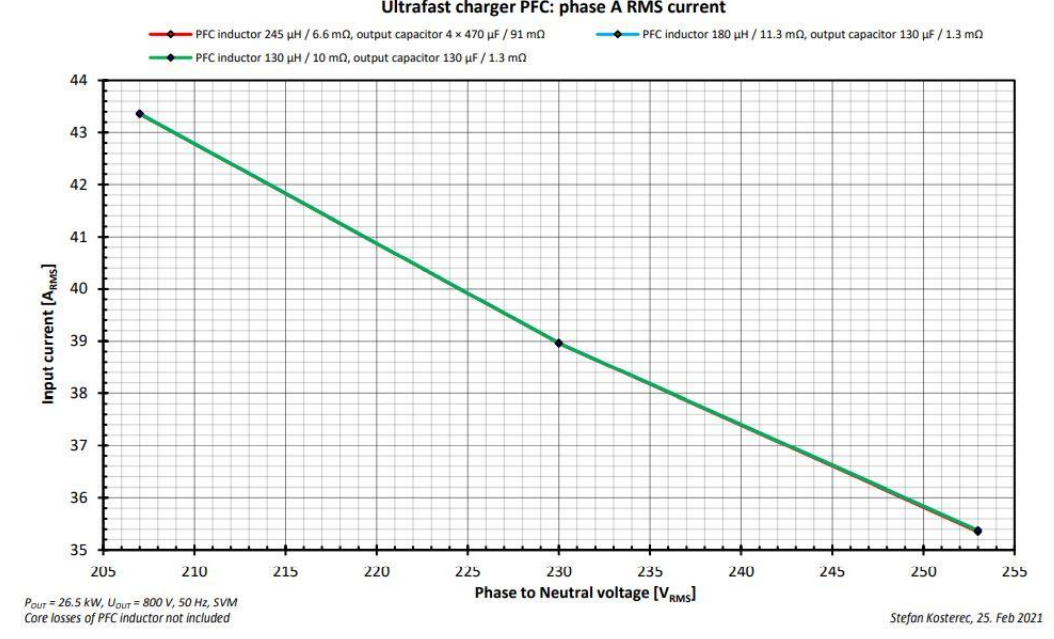
图17. 输入电流有效值和输入电压值、感值和输出容值的关系。
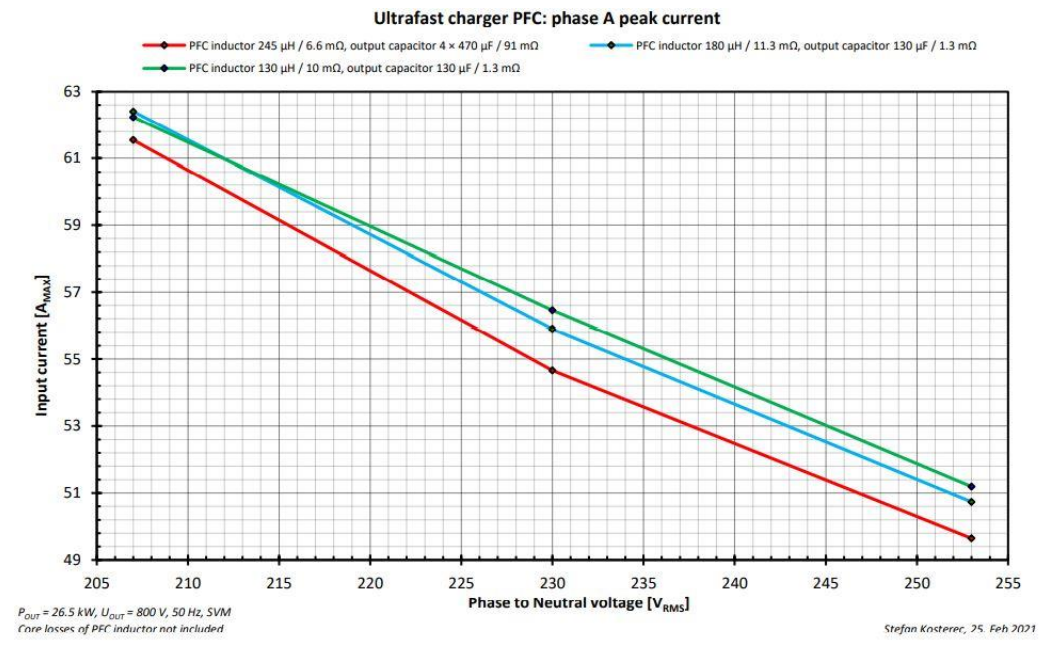
图18. 输入电流峰值和输入电压值、感值和输出容值的关系。
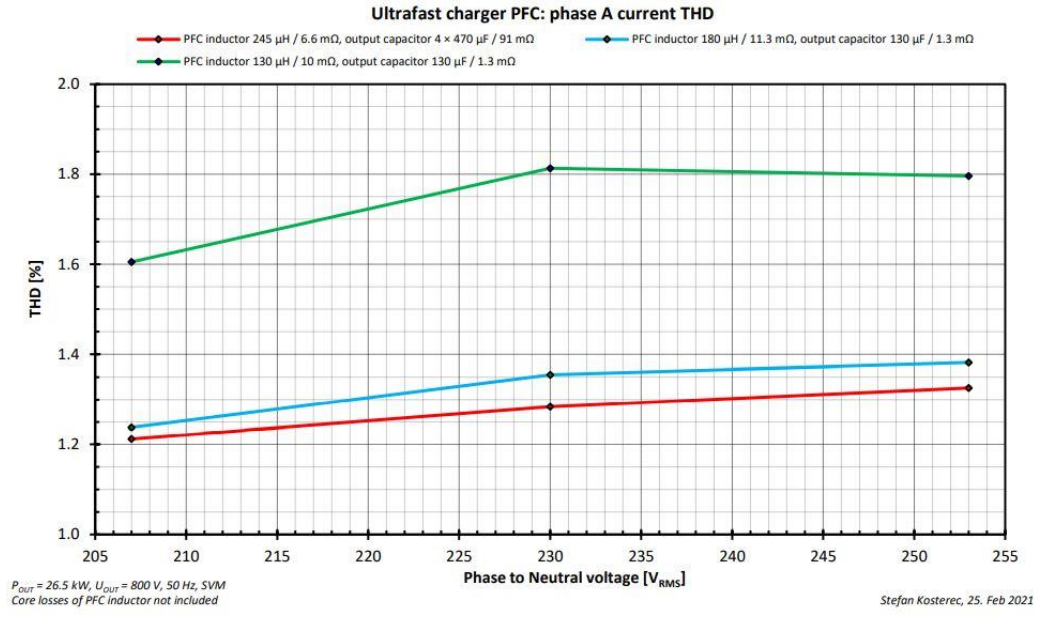
图19. 输入电流总谐波失真(THD)和输入电压值、感值和输出容值的关系。
 最前沿的电子设计资讯
最前沿的电子设计资讯