
DAB 转换器控制策略的实施遵循与 PFC 类似的过程。在本章节中,我们将讨论转换器的控制算法以及磁通平衡技术。在撰写本文时,需要重新设计转换器的 Simulik 模型,以便为 HDL 编码器做好准备,并且 DAB 的平均模型尚未最终确定(我们尚处于图 4 的步骤 6 中)。
从控制算法开始,在可用控制技术中,最著名的技术可能是固定频率相移技术。图 11 显示了这些技术的分类,其中单相移 (SPS) 是最简单的一种。事实上,控制器的简单性正是该技术的主要优点,但其代价是转换器中电流循环的增加,以及在更严格的工作范围内才可能实现零电压开关 (ZVS)。这两个缺点肯定会影响系统的效率。
基于 SPS 的两种替代方案是扩展相移 (EPS) 和双相移 (DPS) 技术,它们能够更有效地利用转换器,减少了循环电流并扩展了 ZVS 的工作范围。但这些改进的代价是系统需要添加额外控制,增加了复杂性。
最后,三重相移 (TPS) 技术是 SPS、EPS 和 DPS 的统一版本。从这个角度来看,SPS、EPS 和 DPS 都可以从 TPS 派生得到,可以视为 TPS 的特例或子情况。图12-14 分别说明了 SPS、EPS 和 DPS 的工作原理。
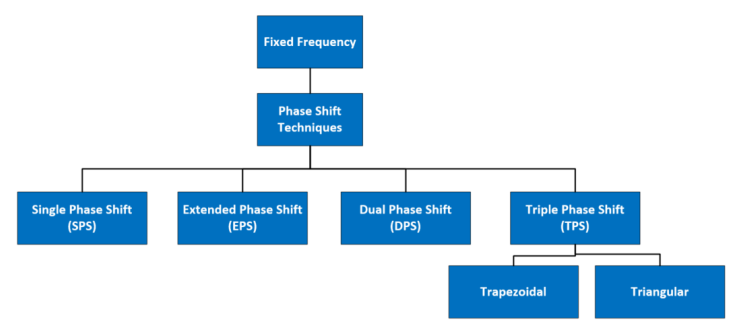
图 11.不同相移技术的分类。三重相移 (TPS) 是其他技术的统一版本,其中的每一种技术都可以视为 TPS 的子情况。
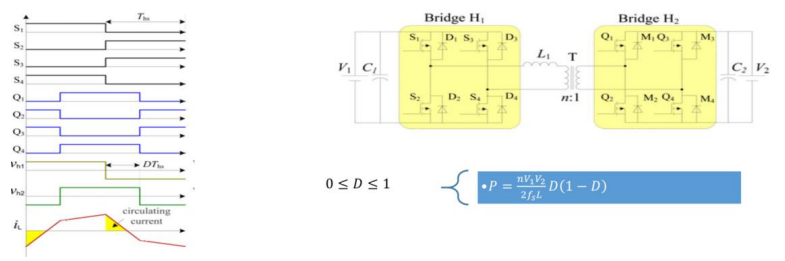
图 12.单相移 (SPS) 技术。(资料来源:“用于高频链路功率转换系统的双有源桥隔离型双向 DC-DC 转换器概述”[9])
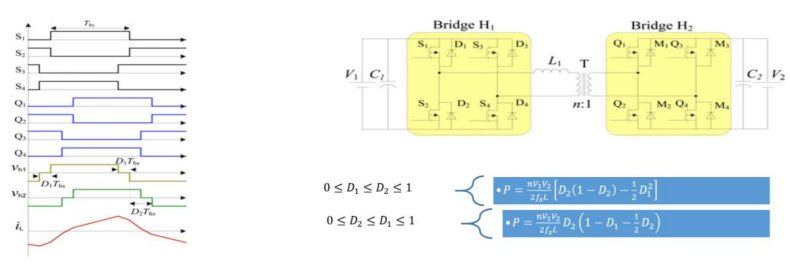
图 13.双相移 (DPS) 技术。(资料来源:“用于高频链路功率转换系统的双有源桥隔离型双向 DC-DC 转换器概述”[9])
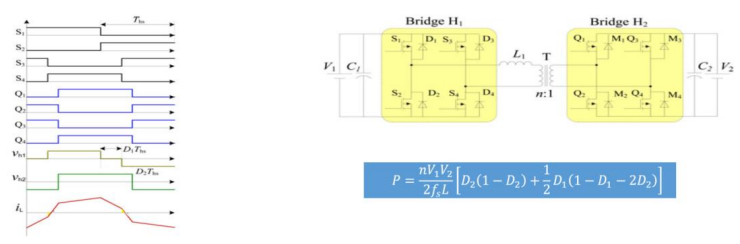
图 14.扩展相移 (EPS) 技术。(资料来源:“用于高频链路功率转换系统的双有源桥隔离型双向 DC-DC 转换器概述”[9])
在本系列文章的第四部分中,我们注意到,DAB 转换器的电源仿真是使用 SPS 进行的。稍后,我们将在硬件原型上测试更先进的技术,并评估每种技术将带来的优势。
最重要的可能改进将是转换器效率提升。此外,还有可能降低变压器中的励磁峰值电流 (IM),这将允许使用更紧凑的变压器和电感。
DAB 的控制原理如图 15 所示。控制器的目标是为电池生成所需的输出电压或电流。
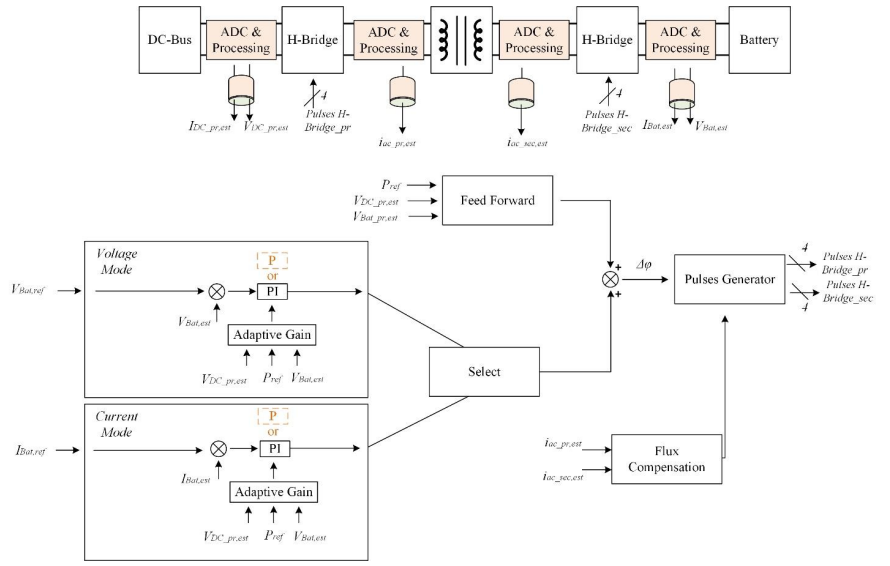
图 15.DAB 控制算法的框图。变压器磁通平衡算法也包含在其中。
基本概念很简单:将测得的输出电压(或电流)和目标值都馈送至输入 PI 控制器。PI 控制器的输出试图通过产生所需的 Δφ(即 DAB 的初级交流电压和次级交流电压之间的角度相位差),消除它们之间的误差,以驱动初级侧和次级侧的 PWM。由于输出电容的存在,控制环路很慢,但考虑到电池充电的缓慢动态行为,这不是问题。
需补充说明的是,自适应 PI 增益对补偿陡峭的 Vout/ΔΦ 斜率的重要性。可使用纯比例控制器(相对 PI 而言)作为替代方案。不过,工程团队需要对这方面进行进一步研究。
DAB 控制算法中一个值得详细阐述的有趣部分是通量平衡功能。这项技术在第四部分中介绍过,它可以补偿换流变压器中的任何直流分量,防止励磁电流的累积和磁芯饱和。
图 16 显示了用于在 25 kW DAB 变压器中实现磁通补偿概念的 Simulink 模型。该模块具有三个输入和一个输出。初级和次级变压器电流和同步 (sync.) 脉冲是该模块的输入。该模块的输出用于调整变压器初级侧 PWM 的占空比。

图 16.磁通补偿框图。
磁通平衡模块由变压器的次级 PWM 同步脉冲触发(在转换器的开关频率下),这意味着馈入模块的交流电流所需的采样频率应该(至少)是转换器开关频率的两倍。具体来说,同步脉冲是用于驱动次级侧第一个桥臂的高压侧开关的那些 PWM 的脉冲。然后借助采样的输入电流,通过简单的计算得到 DAB 变压器的励磁峰-峰值电流。
随后,由相同的同步脉冲触发采样保持 (S&H) 电路,计算要复制的励磁电流的开关平均值。最后,将估计的励磁平均电流馈送到比例 (P) 控制器,该控制器将生成调整初级侧 PWM 占空比的命令。图 17 显示了在仿真中实现的通量平衡算法的功能。
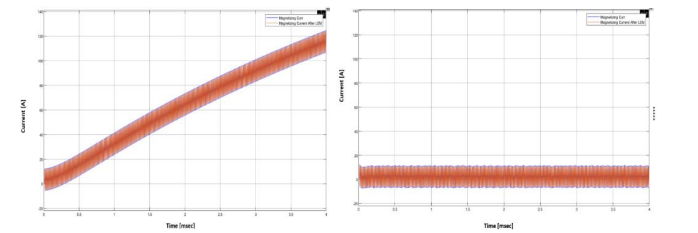
图 17.当 DAB 的磁通补偿算法无效(左)和有效(右)时,仿真的变压器励磁电流 (IM)。当没有运行磁通平衡技术时,剩余直流电流会在每个开关周期内累积,最终会使磁芯饱和。
有效实施磁通平衡技术的一个关键因素是所需的电流采集带宽。如上所述,待测和待作用电流的开关频率为 100 kHz,因此系统至少应该能够在 200 kHz 下进行测量。所以值得运行仿真,以确保所选电流传感器不会引入明显的测量误差,从而破坏磁通补偿实施。
所选电流传感器 (LEM) 指定带宽为 300 kHz。必须考虑到,当采样频率接近 300 kHz 时,会出现增益衰减,并且与任何采集系统一样,可能会出现相位滞后。因此,尽管 300 kHz 乍看之下似乎提供了足够的空间,但还是建议运行仿真。使用/不使用有限 LEM 带宽的采样电流如图18 和 19 所示。(请注意,在本例中,我们尚未激活磁通补偿,因此励磁电流增长非常大。)
在图 19 中,可以观察到幅度和相位存在非常小的误差,但几乎可以忽略不计。算法中包含的两次采样方法(每个开关周期测量两次电流)也会有助于减轻误差。无论是哪种情况,我们已经在图 17 中看到磁通平衡可正常工作。
下示仿真应该在图 17 中给出的结果之前运行或同时运行。因此,可以使用带宽约为 300 kHz 的传统 LEM 传感器。图 20 说明了估计的开关平均电流、实际励磁电流 (IM) 以及同步脉冲。
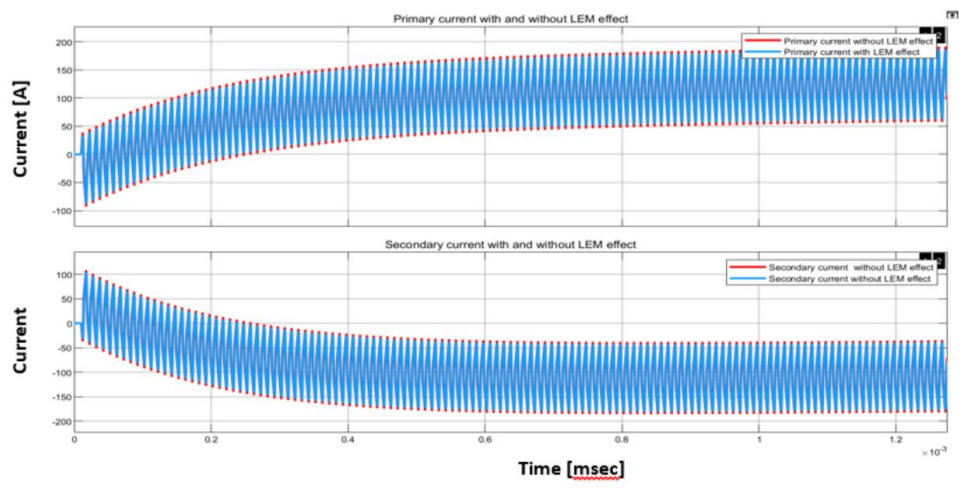
图 18.带/不带 LEM 电流传感器效应的初级和次级电流测量。磁通平衡算法在此仿真中不工作。
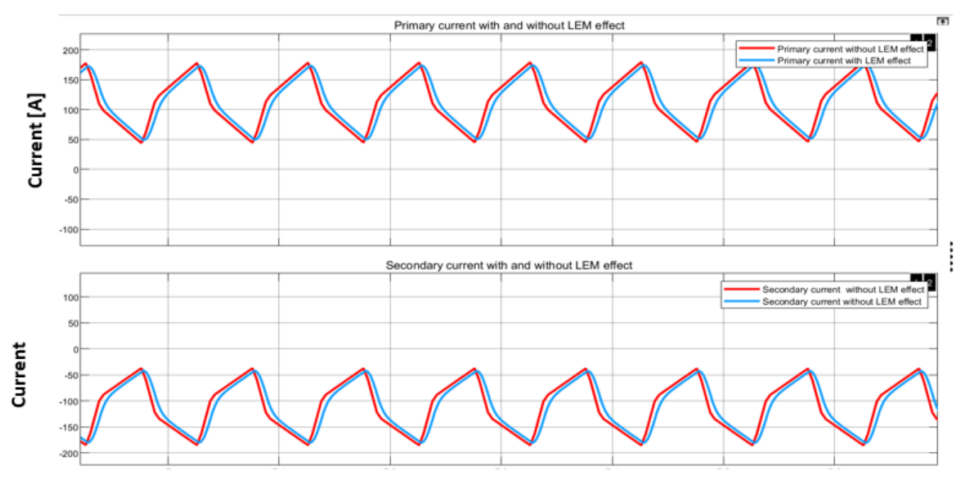
图 19.带/不带 LEM 电流传感器效应的初级和次级电流测量。
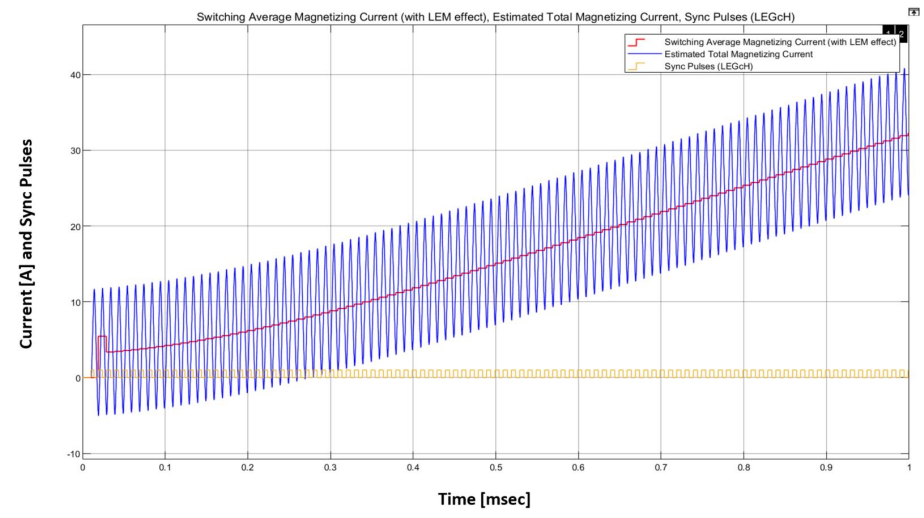
图 20.估计的总励磁电流(带 LEM 电流传感器效应)、估计的开关平均值(带 LEM 传感器效应)和同步脉冲。磁通平衡算法在此仿真中不工作。
 最前沿的电子设计资讯
最前沿的电子设计资讯