
我正在检查的电源在其反馈通路中使用光耦来控制其输出电压。这是一种常见、成熟的设计方法,但反馈回路的无条件回路稳定性并不完全确定。
我决定以两种方式测量光耦的传递函数,如下所示。我知道该器件的数据手册提供了这种特性,但我想亲自了解一下(图1)。
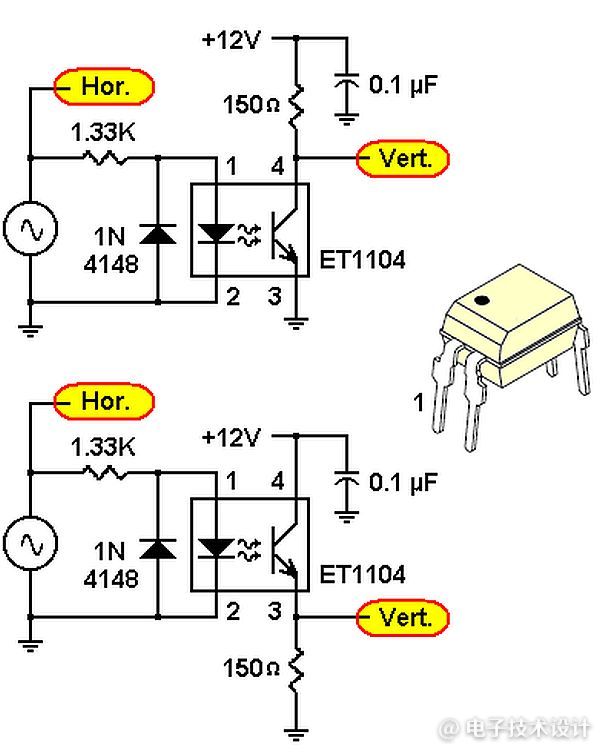
图1:光耦传递函数测试设置。
恰好我手边有1.33kΩ和150Ω两个电阻,为了方便,我使用了它们。一对1kΩ和100Ω电阻也就足够了,但那一刻我只是不想翻找。
这两个测试结果似乎确实证实了数据手册的介绍(图2)。
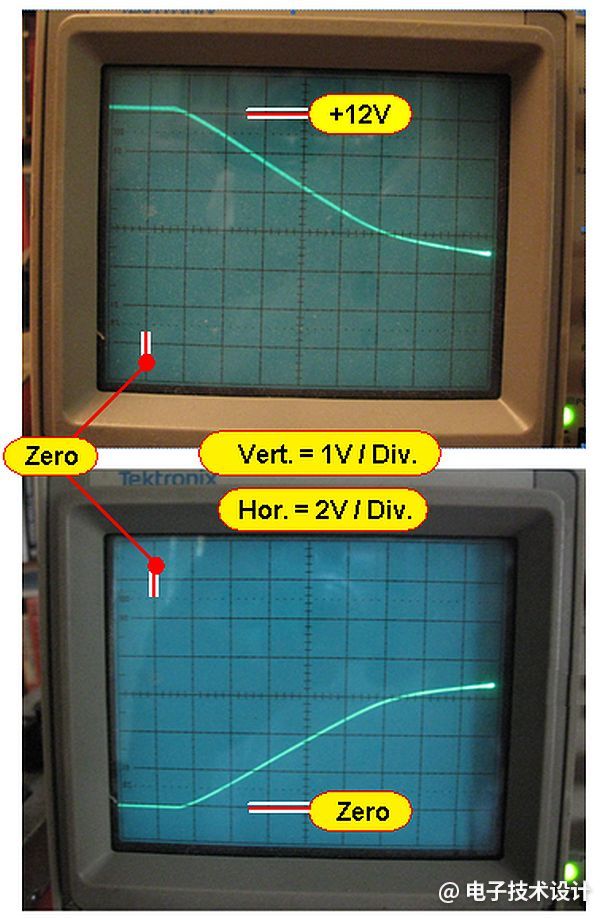
图2:光耦传递函数测试结果。
图2的上部和下部迹线分别与图1的上部和下部草图相配。注意到这两个测试结果具有对称性令人欣慰。然而,经过一些心理反思,我意识到有一个回路增益陷阱需要注意。
使用图2的下部迹线,测量传递函数斜率,可以看到以下内容(图3):
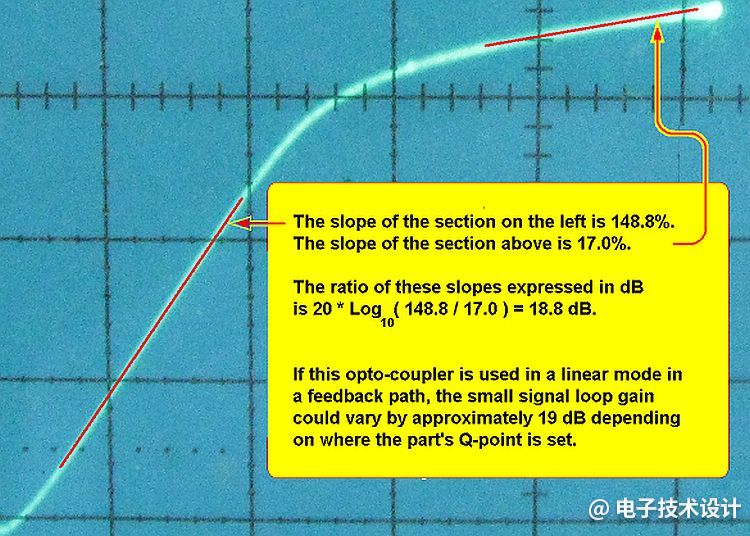
图3:传递函数的特写检查。
图中文字:
左侧部分的斜率为148.8%。
上侧部分的斜率为17.0%。
这两个斜率以dB表示的比率为20*log10(148.8/17.0)=18.8dB。
如果将此光耦在反馈通路中以线性模式使用,则小信号回路增益可能会变化大约19dB,具体取决于该器件静态工作点(Q点)的设置位置。
光耦的“线性”特性不能太从字面上去理解。该器件的传递函数不会发生改变或类似情况,但输出对输入的一阶导数,即输出对输入的斜率,会随着设置器件静态工作点的位置而变化。我所检查的器件的可变性接近19dB。
如此大的增益变化可能会对反馈回路的整体传递函数产生“跺脚”(rompin'-stompin')效应,从而可能会将边缘稳定的反馈回路推入条件不稳定状态。
所有这一切的注意事项是,确保检查为自己选择的任何光耦的真实斜率,以及选择将其静态工作点设置的位置。
(原文刊登于EDN美国版,参考链接:Linear opto-couplers and the loop gain 'booby trap',由Franklin Zhao编译。)
 最前沿的电子设计资讯
最前沿的电子设计资讯