
图片来源于Mark König , Unsplas
这篇文章将从物理学的角度,从物理学到人工智能来介绍物理信息神经网络。
让我们从这里迈出第一步:
我们已知物理学中的世界是如何运行的。通过运用科学的方法可以提出假设,我们说明一个具体的现象是如何发生的,然后再设计一个可控的实验,通过实验数据来证实或证伪这个假设。
可以说,物理学和自然演化的进程是息息相关的,我想起在大学时一个教授用下面这句话开始自己的报告:
赫拉克里特斯说:“万物皆动。”我对此深信不疑。但是,如何运动的呢?
而这便是物理学在试图解答的问题。“万物”如何“动”呢?
人们用特定的方程——为人熟知的微分方程来描述万物运动的方式。让我们先来试图理解什么是微分方程。
“微分”描述了一类与减法有关的东西。
一个函数的导数在物理学当中有着特殊的意义。
举个例子,速度表示的是空间对于时间的导数。让我们考虑如下实验:一个物体沿着一根一维线条运动。

也就是说这个蓝色的小球正在沿x轴运动。通常,我们把初始点设置为0。当这个小球运动时,它的位置会随着时间改变,假设这个位置随时间变化的图像如下:
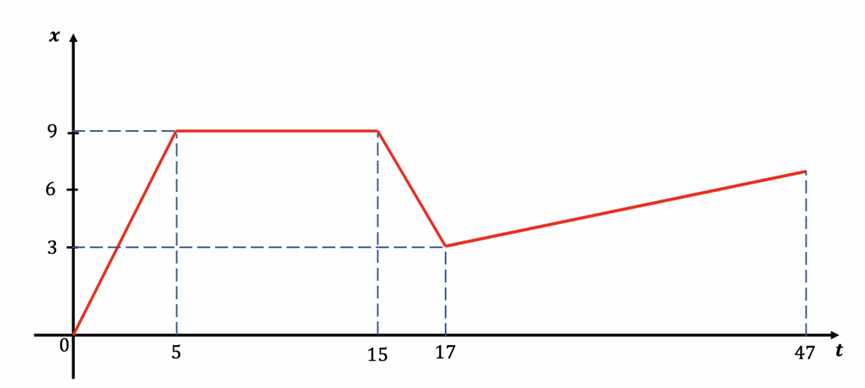
于是这个运动可以被描述得更加清晰:
A.在时刻0至时刻5之间,位置从0变化至9:小球向前运动。
B.时刻5至15,位置没有改变:小球静止了。
C.时刻15至17,位置由9至3:小球往回运动。
D.时刻17至47位置由3至6:小球又前进了。
这个小球何时如何改变自己的位置是不是被清晰定量了呢?甚至位置变化量都很清楚。其实这便是速度的信息,我们用下面的表达式来描述:
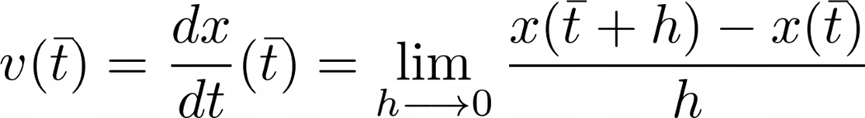
看起来好像有些复杂。但其实速度只是两个非常相近的时刻对应的(表达式中h趋于0的极限)位置变化量除以两个时刻的差(h),所以我们用微分方程来描述。换句话说,速度是用时间间隔归一化后的位置瞬时变化量。
如果在某个特定时刻,位置有一个剧烈的增加,意味着其导数是非常大的正数;位置没有改变时,导数为零;位置减小,导数为负。
在上面的例子当中,每段位置的变化是线性的,也就是说时刻段0-5、5-15、15-17、17-47间的速度各自不变。
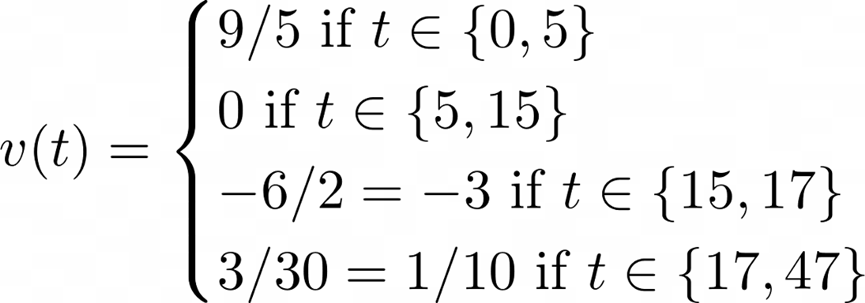
以t=0至t=5为例,期间对于每一时刻t,位置的瞬时变化量都是9/5,其他时段亦可以用同样的意思理解上面的函数。
上面的例子非常简单,让我们来考虑下面这个例子看看:
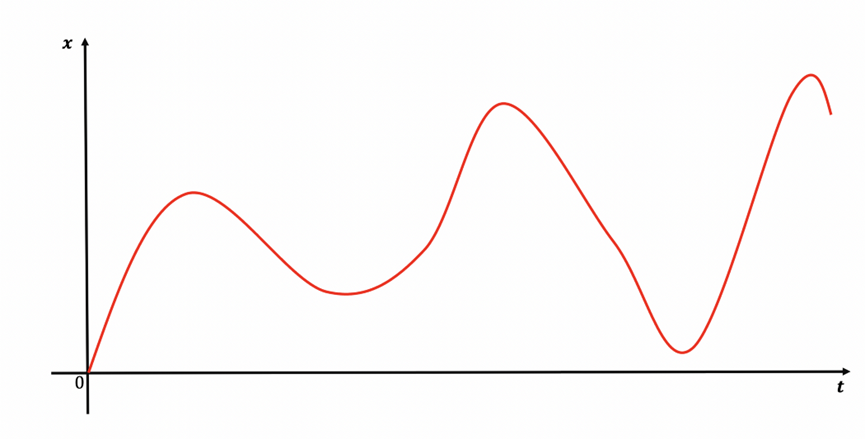
这样的轨迹就很难建模了,也没有解析的方法去计算导数:你只能用数值的方式来计算——在所有时间点用公式(1)给出导数。顺便一提,我想你已经完全准备好面对残酷的现实:
现实世界中所有的微分方程都是用数值软件求解的。
但数值求解可能需要执行千万次迭代。不仅如此,还需要高级的方法来求解微分方程,像有名的龙格-库塔(Runge-Kutta)方法,往往会集成于很复杂的软件当中(比如用于有限元方法的POGO),这些软件:
计算成本高
经济成本高
需要专业知识
时间成本高(以有限元方法为例,往往花费数分钟至数小时不等)
而上述的问题甚至不是最糟糕的。难过的是会出现不适定(ill-posed)的情况。下面我举个例子。
比如要求解x和y的问题:
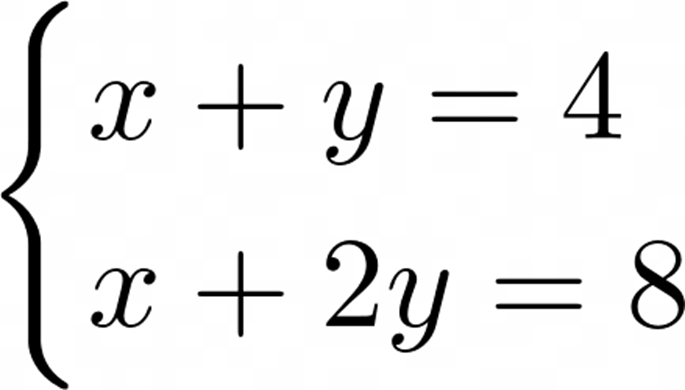
是不是挺简单?
• x+y=4
• 于是 x+2y=x+y+y=8
• 4+y=8
• 得到 y=4
• x=0
方程组的解为 (x,y) = (0,4),此时这个问题是适定的。因为满足这种条件的解是惟一的,也就是上面得到的解。
但以下问题就不一样了:
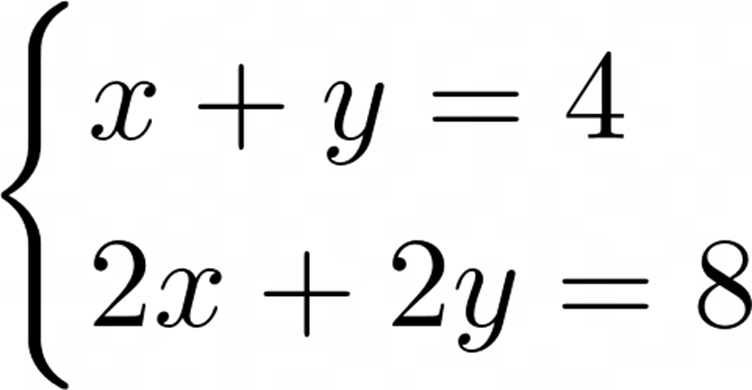
两个方程其实是一样的!虽然 (x,y) = (0,4)还能作为一个解,但是(1,3)也可以,这个方程组实际上有无穷多个解。这个问题就是一个不适定问题,对于这样一个确定的问题,具有不只一个解(实际上有无穷多个解)。
如果是求解下面这个问题:

这类所谓的反演问题可以用于从位移图推导出速度图,而上面的这个反演问题可以用于超声波探测中表征材料中的一个侵蚀缺陷。即使是最完美的实验设置(无限多个传感器),这个问题也是不适定的。换句话说就是,信息不能够推导出一个唯一且可靠的速度分布图(
现在说说人工智能(AI)。
这句话可以很简单地介绍人工智能:
人工智能算法不需要具体的程序就可以执行特定的任务。
自动驾驶汽车在没有数学和明确训练情况下,也可以在任何人走到车前时刹车,这是因为它通过了百万人的“训练”。
准确地说,所有人工智能算法都依赖于损失函数(Loss Function)。
这个特定的函数用于表示目标值(target,希望输出的值)和算法输出值之间的差,需要通过优化来达到最小值。
假如给定一座具有特征的房子,希望预测其花费(一个很有名的房产数据集问题)。这是一个由输入空间至连续空间的回归(regression)问题。
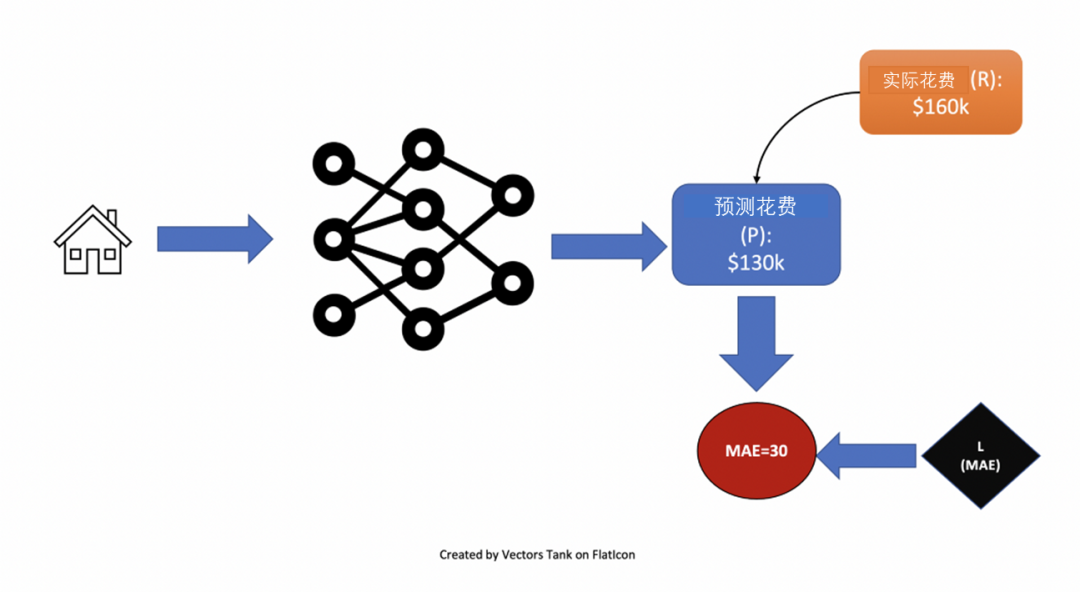 图源作者
图源作者
如果给出的预测价格为130k而实际价值为160k,那么平均绝对值误差MAE定义为:
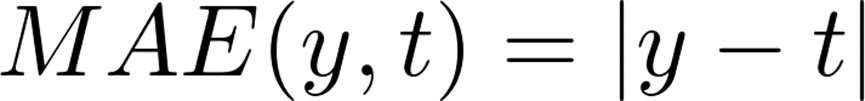
在这个问题中为30k。
这个式子表示,我们的模型是一个命名为
如果有许多的房屋
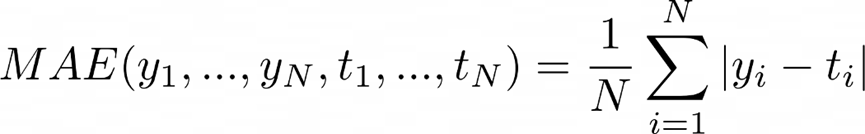
损失函数依赖于建立模型的一系列参数W。损失函数越低,就说明模型建立得越好。
于是,损失函数就会不断优化,某种意义上降到越低越好。参数会被不断迭代,来使损失函数降到最低(局域最小值)。
如果你看到这里:
你值得一阵掌声
你可能会有疑问:人工智能(神经网络)和微分方程(物理)到底有什么关系?
在回答这个问题之前,我们需要了解另一个概念——正则化(regularization)。
在上一部分,我们了解到所有机器学习算法最终都是一个优化问题。意思就是去寻找最小化损失函数的最佳参量组
但会出现一个问题,可能这个解在训练集中达到最佳,但是并不适用于测试集(过拟合),此时的最佳值只是局域最佳的。
再深入解释一些:
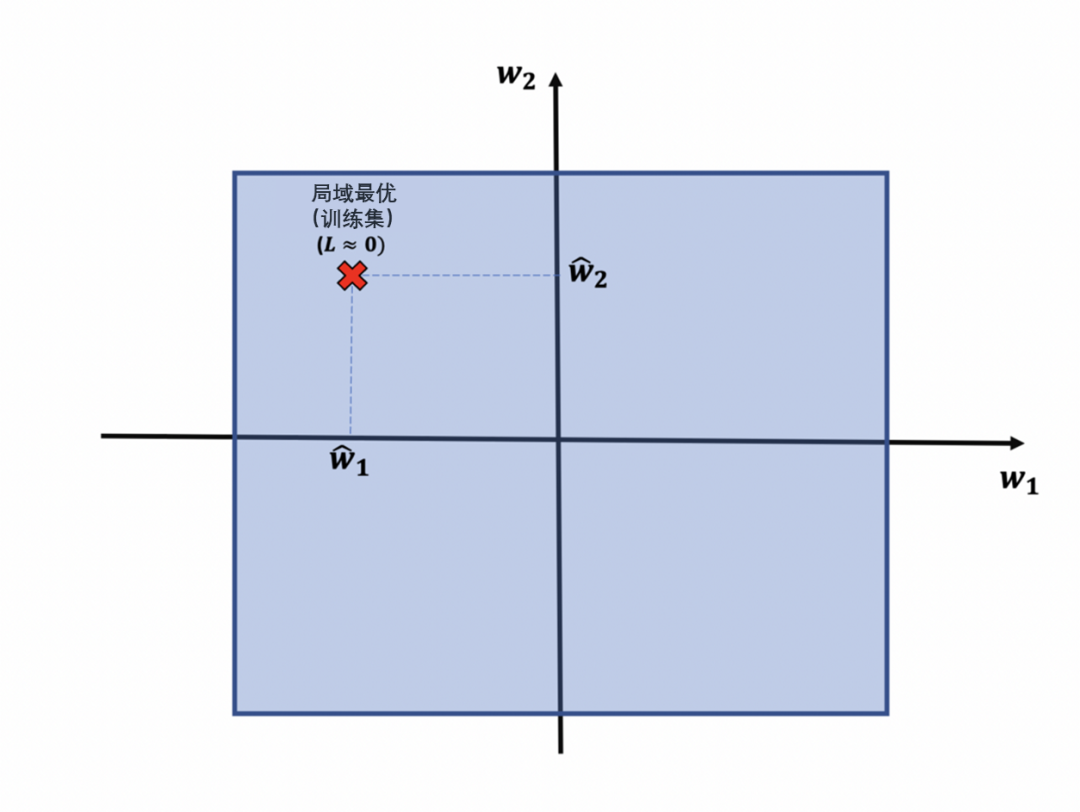
假设初始模型由
 图源作者
图源作者
获得的参数训练集中应用的损失函数得到的损失值L接近0.
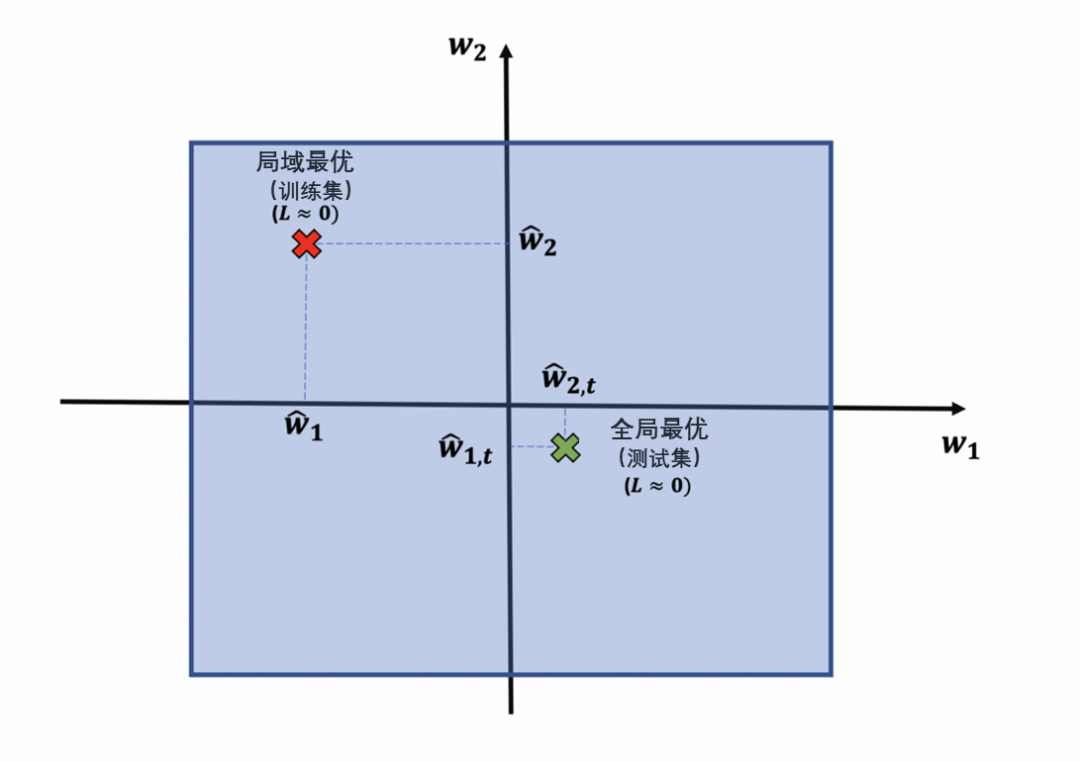
如果将这个参数组合应用于测试集(一系列新数据),损失函数变得非常大。就说明损失函数的定义并不准确,其实在这个问题中,真正最优解如下:
 图源作者
图源作者
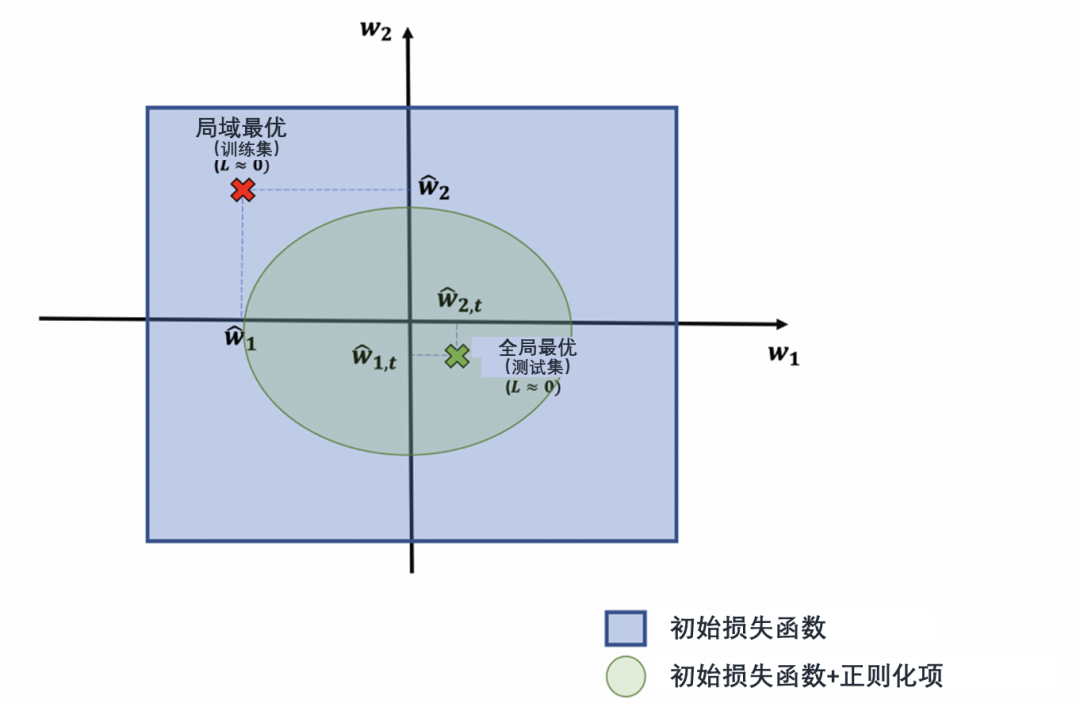
那么如何避开红色标记的错误点而得到最优点(绿色标记)呢?
 图源作者
图源作者
如果算法只在绿色圆圈中“寻找”就好了,这样就不会落入错误的红色圈套(局域最优)了。
这就是正则化——修改损失函数使得其空间解被限制,从而更可能求解出全局最优而非局域最优。
还记得上面方程(2)所表示的反演问题吗?一些学者正在尝试求解。
初始时,在一些特定位置已知位移(u),他们希望在算法未知区域插值u来获得v。也就是说,给定新的t、y和x,可以获得对应新的位移,从而获得新的速度分布。
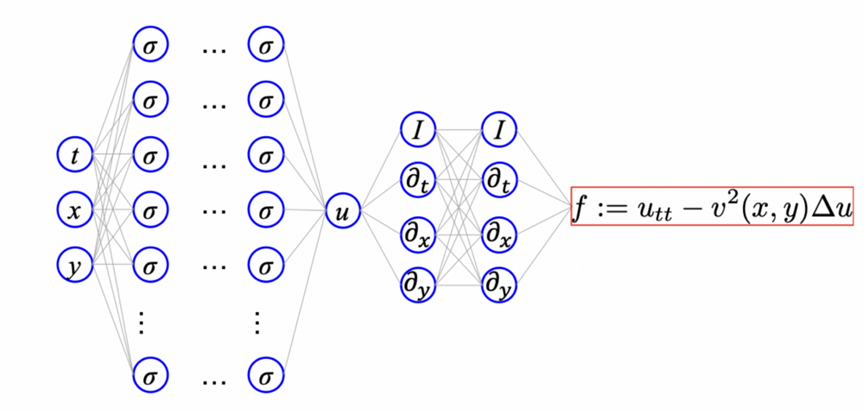
现在对于这个方程的解法存在许多争议,因为这个问题不是适定的,也就是说即使人们发现了一个解,也不能确定其是否是唯一的。不仅如此,还有许多物理学限制无法求解。
他们希望通过限制位移满足波函数方程(2)来产生位移,与损失函数结合:
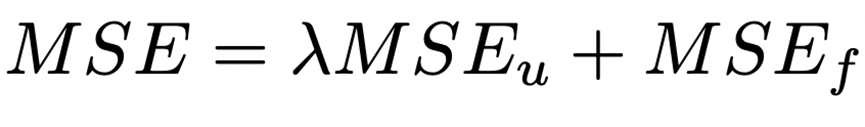
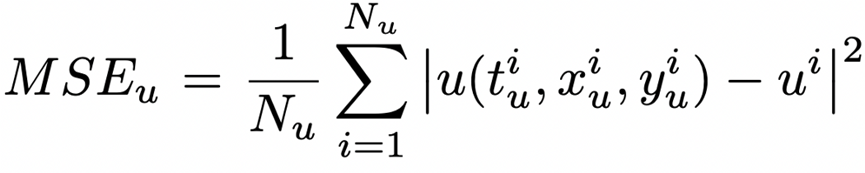
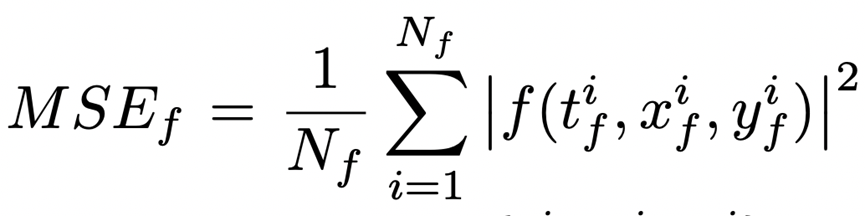
其中
这表示什么呢?简而言之,代表了一个正则化过程:
他们在通过限制损失函数范围(排除不符合微分方程的解)帮助算法找到最优解。
神经网络是如何获得“物理信息”的呢?通过微分方程正则化而已。
在文末,我想说:
物理信息神经网络不过是通过微分方程正则化损失函数的神经网络而已。
通过几分钟的阅读,本文可以总结为几个方面:
· 损失函数是什么(第2部分)
· 正则化是什么(3.1部分)
· 微分方程是什么(第1部分)
· 物理信息是什么(3.2部分)
希望你对物理信息神经网络有了一定的了解~
作者:Piero Paialunga
翻译:zhenni
审校:C&C
原文链接:
https://towardsdatascience.com/physics-and-artificial-intelligence-introduction-to-physics-informed-neural-networks-24548438f2d5
 最前沿的电子设计资讯
最前沿的电子设计资讯