如同上文的结论，匹配带宽与要匹配的两个阻抗相关，阻抗比越大，匹配带宽越小。阻抗越接近，匹配带宽越大。那么对于一个阻抗相差比较大的网络，我们是否可以通过多个依次递进的阻抗变换来实现高低阻抗的过度？答案是肯定的。《微波工程》第5.5节引入了小反射理论给出了详细的证明，想了解详情的同学可以查阅学习。我们直接上重点：巴特沃斯型多节阻抗变换器和切比雪夫型多节阻抗变换器。 巴特沃斯响应最先由英国工程师斯蒂芬·巴特沃斯（Stephen Butterworth）在1930年发表在英国《无线电工程》期刊的一篇论文中提出的，其在接近设计频率处，相应尽可能的平坦，因此又叫做最平坦响应，又由于其系数满足二项式系数，也叫做二项式响应。名字也够多的，记住下面的波形就是最平坦/二项式/巴特沃斯的响应曲线。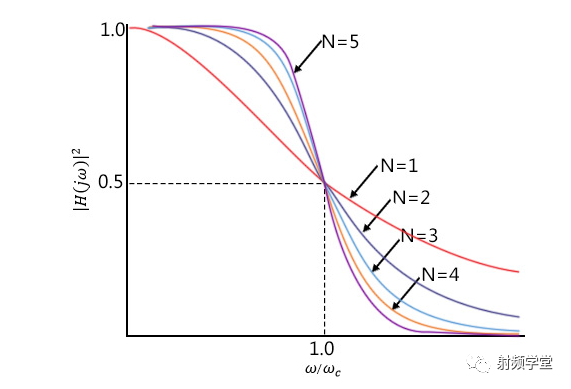 
巴特沃斯型多节阻抗变换器的反射系数Γ 满足下面公式。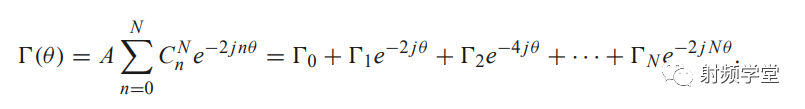 
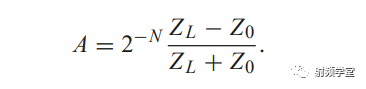在设计的时候，可以相对带宽的需要确定阻抗变换器的节数N，然后根据阻抗公式从Z0开始依次求出每一节所需要的阻抗值。 相对带宽公式： 
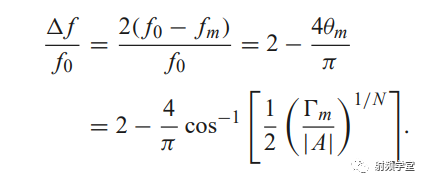阻抗公式： 
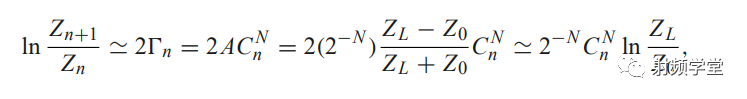巴特沃斯型多节阻抗变换器的反射特性如下图所示：
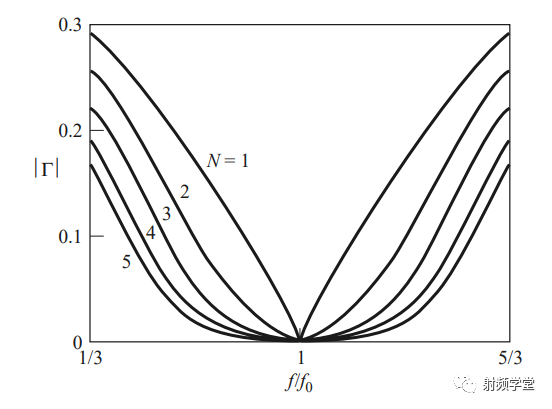
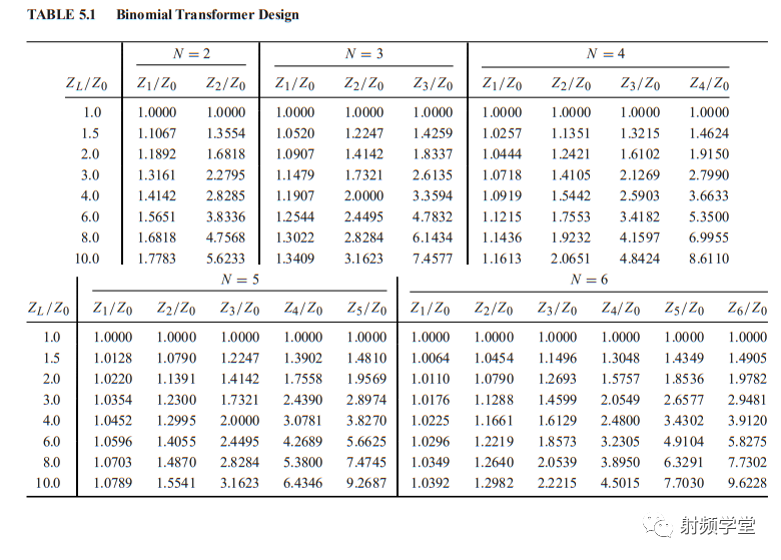
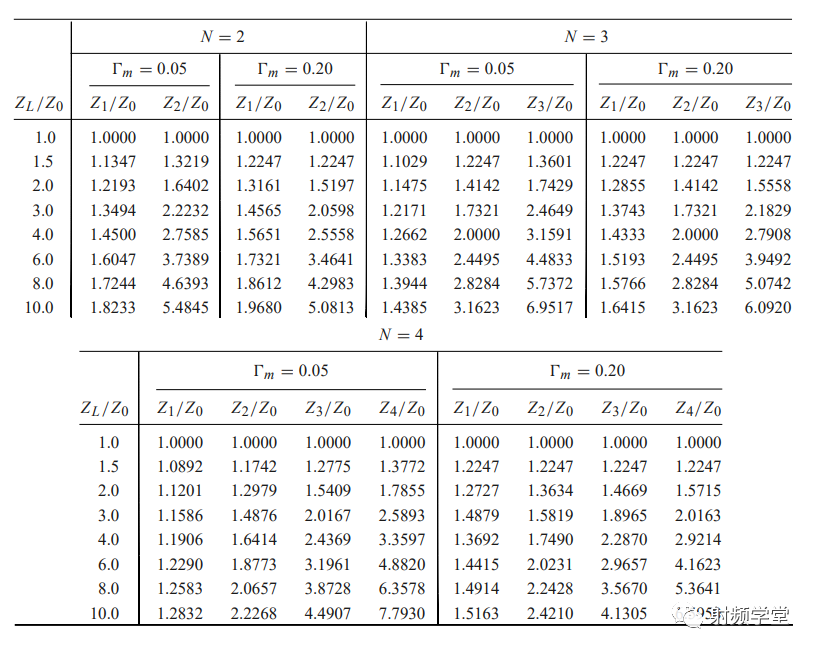
理论上我们可以根据巴特沃斯函数做出无数节阻抗变换器，但是这样也意味着体积的无限扩大，射频设计是一个多方面因素平衡的结果，一般情况下，3-5节也就够工程应用了，抛开复杂的计算，我们可以通过查表来快速完成，当然感兴趣的同学也可以直接写代码做个小APP来辅助设计。 巴特沃斯阻抗变换器设计表（来自《微波工程》）
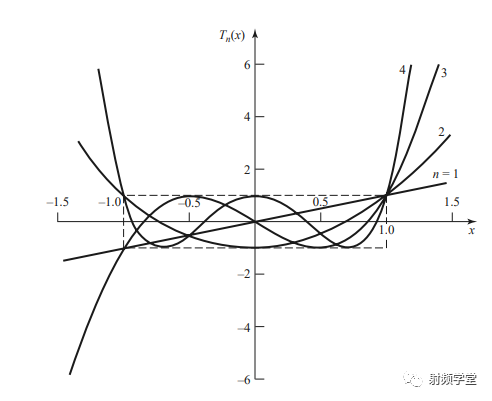
另一种比较常用的多节阻抗变换器是基于切比雪夫响应的阻抗变换器，切比雪夫多项式是以俄国著名数学家切比雪夫(Tschebyscheff，又译契贝雪夫等，1821一1894)的名字命名的重要的特殊函数，其通带内的响应以等波纹特性实现最佳的带宽匹配，因此又叫做等波纹响应阻抗变换器。
切比雪夫多节阻抗变换器的反射系数Γ 满足下面公式
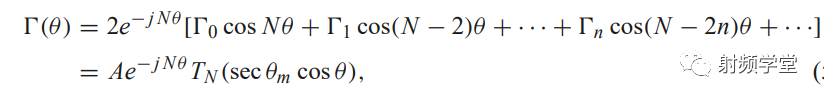
Tn就是切比雪夫多项式
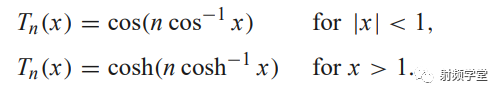
设计切比雪夫多节阻抗变换器时，首先根据通带内所允许的最大反射系数Γm确定多项式的系数 |A|，
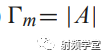
然后根据相对带宽公式求得所需要的节数。
θm可以由下面公式求得。
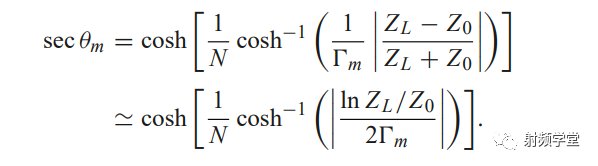
然后依据下面公式从Z0依次求出每一节的阻抗值。
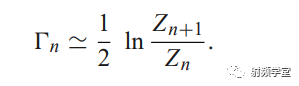
同样的，感兴趣的同学可以写代码做个APP来辅助设计，或者直接查表就可以了，《微波工程》给出了2-4节不同Γm对应的阻抗列表，日常设计这个表足够了。
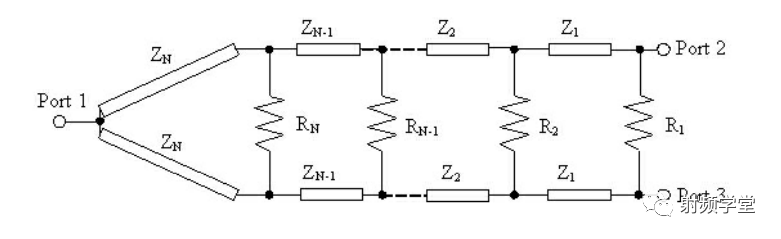
类似于单节阻抗变换器在功分器和耦合器中的应用，多节阻抗变换器也可以用来拓宽功分器和耦合器的带宽。最常用的方式如下图所示：
宽带威尔金森功分器
威尔金森功分器中四分之一波长线用多节来代替，利用巴特沃斯多项式或者切比雪夫多项式来完成多节阻抗来拓宽带宽，原理图如下图所示。
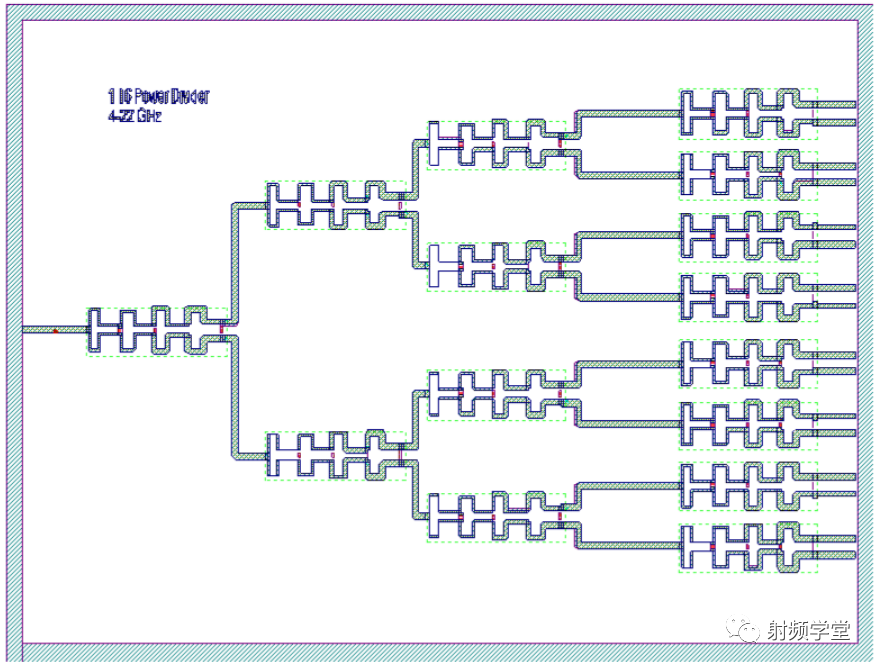
在AWR自带的仿真案例中，给出了1：16的超宽带威尔金森功分器设计，感兴趣的同学可以学习一下：菜单栏 Help > Open Examples>16_Way_Power_Divider
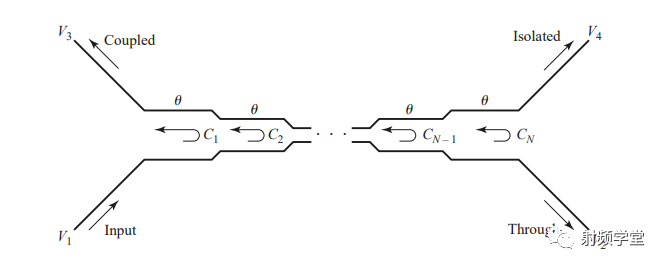
宽带耦合线型定向耦合器 耦合线型定向耦合器也可以采用多节结构来增加带宽，每一节的长度时1/4波长，和多节阻抗变换器类似，也可以设计成切比雪夫型或者巴特沃斯型，其原理图如下图所示。
最前沿的电子设计资讯
