
宏观热力学体系的相变临界行为一直是统计力学研究的核心问题之一。临界行为之所以重要和引人入胜是因为体系在临界点处表现出较非临界点处非常奇特的性质:内部关联长度发散导致体系相较于其它非临界点处出现巨大的热涨落,进而导致刻画体系特征的各种响应函数(对应二阶矩,与涨落有关)在该点呈现出奇异性(发散或间断点等非解析性)。本文将以气液连续相变,平均场近似下Ising模型的连续相变,以及更为一般的Landau关于连续相变的唯象理论 — 二级相变理论为例,具体计算在每种情形下各种热力学量和响应函数的临界行为,这个临界行为由一组特征的临界指数标定。然后通过比较这些临界指数我们可以发现这些看似完全不同的体系和处理手法在相变临界点附近呈现出完全相同的物理行为,并由此揭示出相变临界行为的普适性。最后探讨这种普适性与体系内部对称性间的深刻联系。
1气液连续相变
在考虑了分子间的相互作用势能后(即近端排斥远端吸引),我们可以对原始的无分子间相互作用的理想气体状态方程中的压强和体积做修正。修正后最简单的物态方程即为范德瓦尔斯方程。现考虑1mol非理想气体所满足的如下的范德瓦尔斯方程。其中参数,的值依赖于具体物质(比如水分子有水分子的和,氢气分子有氢气分子的和)。我们将利用该方程来研究在临界点处气液连续相变的问题。
因为相变临界点对应于图上的拐点,所以此时压强对体积的一阶和二阶偏导数均为0。容易解出临界点处的体积,温度和压强分别是:
以临界点的状态值作为单位将原始的范德瓦尔斯方程改写成与具体物质无关的普适方程:
为直观起见,【图1】给出了上述普适方程在不同约化温度下的函数图像:
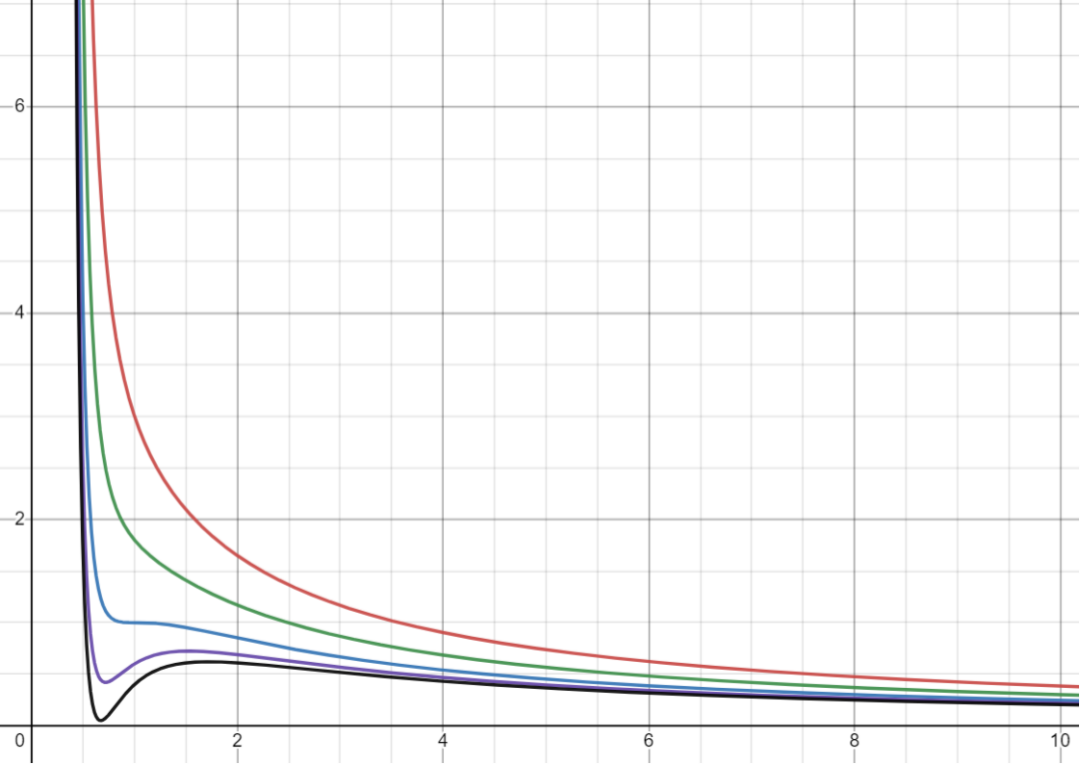
图1 函数图像。其中纵坐标是约化压强,横坐标是约化体积。蓝线代表约化温度,对应相变临界点情形,蓝线上面的绿线和红线代表,下面的紫线和黑线代表
在临界点附近对约化压强,体积,和温度作小量展开到一阶:
其中是临界点附近的小量。所以普适方程可以写成关于小量的形式:
为直观起见,【图2】给出了上式在不同下的函数图像:
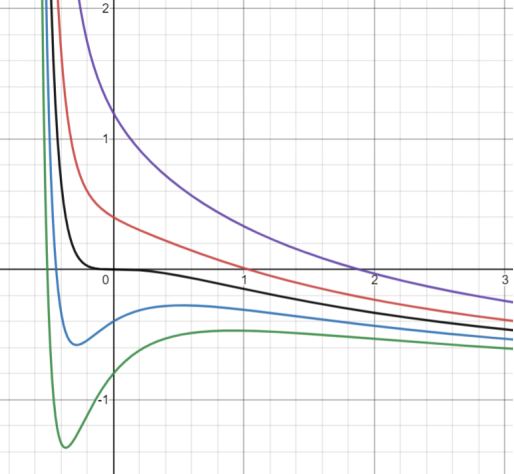
图2 函数图像。其中纵坐标是约化压强在临界点附近展开对应的小量,横坐标是约化体积在临界点附近展开对应的小量。黑线代表在临界温度时的关系,红线和紫线代表临界温度以上的关系,蓝线和绿线代表临界温度以下的关系
将上面关于小量的普适方程在附近泰勒展开:
从【图2】可以看出,在临界温度以下时,即时,由于曲线的非单调性(即关于的多值性),所以体系必然存在气液相变。在相变发生时,根据两相平衡条件,相和相(这里分别指代液相和气相)的温度,压强,和化学势(吉布斯自由能)必须相同。根据两相压强相等的力学平衡条件可以得到:
根据等温线上两相化学势相等的化学平衡条件可以得到:
将间的小量关系代入上式得到:
若假设,则上述方程约化成:
所以意味着和同号,与【图2】()矛盾。所以先前的假设错误。正确的关系只能是,也就是(关于纵轴对称)。注意到这个关系对应到【图1】就是和关于临界体积呈对称分布。
接下来将化学平衡的结果代入到力学平衡的结果得到: , 。这个结果对应于从临界温度下方趋于临界点时,气相和液相间存在体积差, 也就是两相间存在密度差(即两相间不对称,处于有序状态!)。
但当我们从临界温度上方趋于临界点时, 容易看出此时由于 曲线单调, 为了同时满足热学平衡, 力学平衡和化学平衡条件, 只能取 , 对应于此时的气相和液相间不存在体积差, 也就是两相间不存在密度差。所以严格来说,高于临界温度时其实只有一相(叫气相也行,叫液相也行,因为两相间不存在密度差所以两相完全对称,处于无序状态!无法区分谁是气体谁是液体)。所以密度差是个关键的指标,它表征了体系当前进入到了哪种序。我们把这个关键的指标叫做“序参量”!在我们现在考虑的气液相变的例子里,两相的密度差就可以充当体系的序参量。
我们下面看它的临界行为。当从临界温度下方趋于临界点时:
当从临界温度上方趋于临界点时:因为,所以。
所以如【图3】所示,当从临界温度下方趋于临界点时,序参量(密度差)是以的方式趋于0的;当从临界温度上方趋于临界点时,序参量(密度差)恒为0。所以我们得出在气液相变问题里序参量的临界指数是1/2!因为此时序参量(密度差,基本对应吉布斯自由能的一阶导数)在临界温度处连续,所以我们也称这种相变叫“连续相变”。
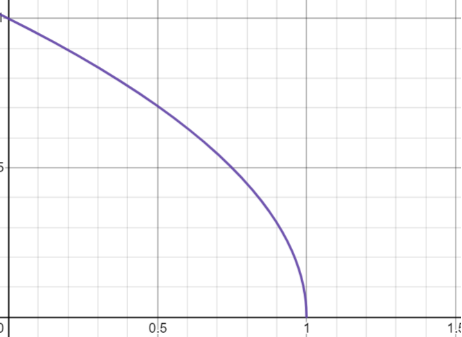
图3 - 序参量(密度差)-温度在临界点附近的行为。纵坐标是序参量(密度差),横坐标是温度。序参量在临界点左侧非零标志着体系进入有序相,右侧是零标志着体系进入无序相
下面看等温压缩率的临界行为:
所以我们发现不管是从临界温度下方还是上方趋于临界点,等温压缩率都是以的方式趋于无穷大(发散)的(见【图4】)!所以我们得出在气液相变问题里等温压缩率的临界指数是1!
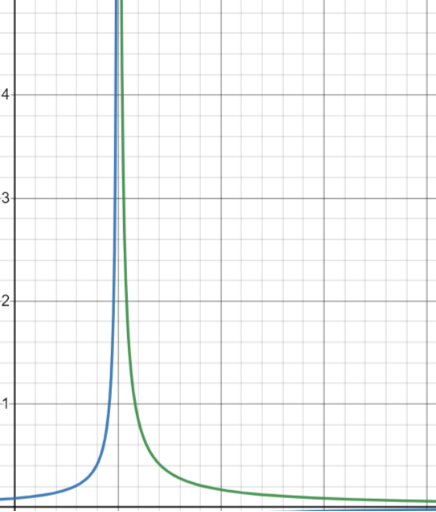
图4 - 等温压缩率-温度 在临界温度附近的发散行为。纵坐标是等温压缩率,横坐标是温度
因为等温压缩率基本上是体积对压强的一阶导数,而体积又基本上是吉布斯自由能对压强的一阶导数,所以等温压缩率基本上是吉布斯自由能对压强的二阶导数。也就是说在临界温度处,吉布斯自由能对压强的二阶导数出现奇异性(发散)!吉布斯自由能对热力学参数的二阶导数一般对应到体系的响应函数。所以此时响应函数在临界点附近出现奇异性。这种连续相变一般被称作“二级相变”。
下面看等容比热的临界行为(由于此时气液相变系统的所有信息是以关于, , 的物态方程而不是以自由能或配分函数的形式给出的,所以这里等容比热的计算相当繁琐,这里直接给出结论):
所以我们发现不管是从临界温度下方还是上方趋于临界点,等容比热都是以的方式发生奇异性(间断点)的!所以我们得出在气液相变问题里等容比热的临界指数是0!
根据先前关于小量的物态方程易知:当固定在等温线(即)时,偏离压强和体积临界值的小量间满足三次方的关系:(见【图5】)。或者用原始的量可以把关系表示成: 。这里的临界指数3也是标定气液相变临界行为的一个特征指标!
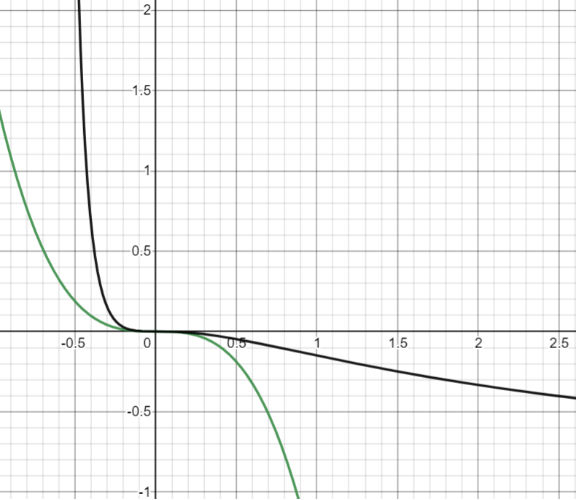
图5 - 纵坐标是压强偏离的小量,横坐标是体积偏离的小量。绿线代表压强相对体积的三次方的临界行为,黑线代表原始未作近似的严格的临界温度上压强-体积的行为。可以发现在坐标原点附近,黑线基本与绿线重合 2平均场近似下Ising模型的连续相变
考虑一个任意维度下的Ising模型。在平均场近似下,我们把Ising形式的相互作用等效成了外磁场的一部分,使得体系被近似成一个等效的“无相互作用”体系。在统计力学的框架下通过对Ising形式正则配分函数的操作,容易得到关于平均磁化的自洽方程。当外场时(也就是考虑自发磁化),临界点附近的平均磁化是个小量。所以将自洽方程关于小量展开得到:
其中特征温度。上述自洽方程其中一个解是,其余两个解是否存在取决于以下方程右侧是否大于0:
当时,方程右侧小于0,故原方程只有这个解;
当时,方程右侧大于0,故原方程除了有的解,还有
这两个解。由于对应的Helmholtz自由能比时的自由能来得高,所以是非稳定态必须舍去。所以当体系从临界温度下方逼近临界点时,的临界行为是:
当体系从临界温度上方逼近临界点时,。
所以如【图6】所示,当从临界温度下方趋于临界点时,序参量(平均自发磁化)是以的方式趋于0的;当从临界温度上方趋于临界点时,序参量(平均自发磁化)恒为。所以我们得出在平均场近似下Ising模型里序参量的临界指数是!这个结果和之前气液相变里序参量(密度差)的临界指数完全一样!
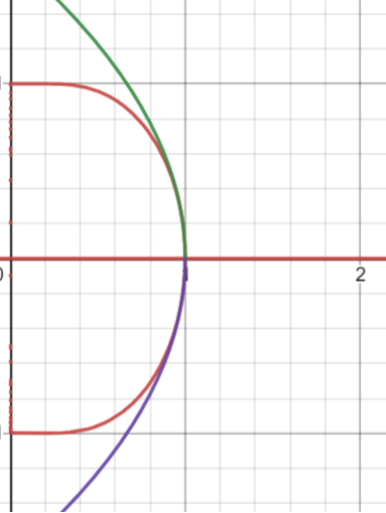
图6 - 在外场时,纵轴代表平均磁化,横轴代表温度。红线是严格按照平均场近似下的自洽方程给出的平均磁化-温度的函数关系,绿线和紫线是按照临界点附近对自洽方程作小量展开近似后出来的结果。可以发现在临界点附近,它们与红线基本完全重合
下面看等温磁化率的临界行为。由于此时需要考虑磁场的变动,所以我们需要使用原始带的自洽方程:
所以体系的磁化率是:
根据之前的结论,当外场趋于0且从临界温度下方趋于临界点时, ,所以:
当从临界温度上方趋于临界点时,, ,所以:
所以我们发现不管是从临界温度下方还是上方趋于临界点,等温磁化率都是以的方式(类似宏观顺磁性的居里定律)趋于无穷大(发散)的(见【图7】)!所以我们得出在平均场近似下Ising模型里等温磁化率的临界指数是1!这个结果和之前气液相变里等温压缩率的临界指数完全一样!
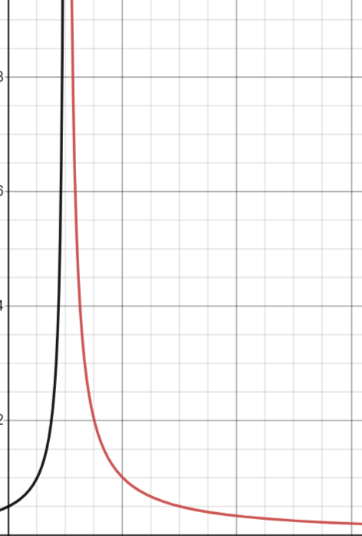
图7 - 等温磁化率-温度在临界温度附近的发散行为。纵坐标是等温磁化率,横坐标是温度
下面考虑无外磁场时比热的临界行为。思路是从Ising体系的正则配分函数出发求得内能,然后通过内能在临界点附近的行为推断出比热的临界行为:
当从临界温度下方趋于临界点时,, ,所以:
所以当从临界温度下方趋于临界点时比热是:
当从临界温度上方趋于临界点时,,,所以容易看出比热是:
所以我们发现不管是从临界温度下方还是上方趋于临界点,比热都是以的方式发生奇异性(间断点)的!所以我们得出在平均场近似下Ising模型里比热的临界指数是0!这个结果和之前气液相变里等容比热的临界指数完全一样!
最后看固定在临界温度上,当外磁场很弱的情况下,和(或)的关系:
因为在临界点附近且很小,所以也很小。所以里宗量很小。所以方程右端可以展开成
所以如【图8】所示,当固定在临界温度时(且外场很小时),磁场和平均磁化或平均磁矩间满足三次方的关系:或。这里的临界指数3也是标定平均场近似下Ising模型临界行为的一个特征指标!这个结果和之前气液相变里偏离压强和体积临界值的小量间满足的关系所对应的临界指数3,即,完全一样!
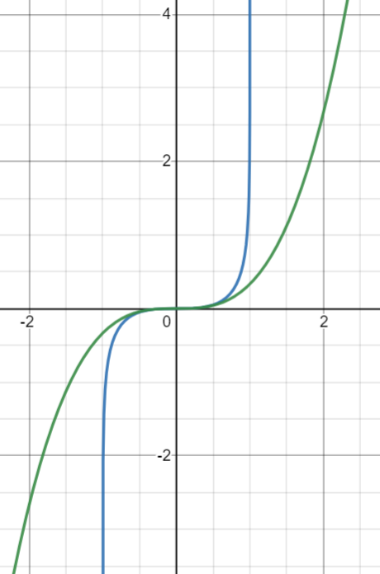
图8 - 纵坐标是磁场,横坐标是平均磁化。绿线代表磁场相对平均磁化的三次方的临界行为,蓝线代表原始未作近似的严格的临界温度上磁场-平均磁化的行为。可以发现在坐标原点附近,蓝线基本与绿线重合 3连续相变的唯象理论 — Landau二级相变理论
从(1)和(2)的分析中可以发现体系在临界点处发生相变的过程其实是一种从高温时的无序态到低温时的有序态的变化过程。其中气液相变例子里的序就是液体和气体的密度差(或体积差),平均场近似下Ising模型例子里的序就是平均磁化。这种序的变化本质上体现出的是体系对称性的破缺,是刻画相变特征的极重要的内禀参数,被叫做“序参量”。所以我们可以唯象地把序参量写进一个叫做Landau自由能的表达式中。假定这个Landau自由能在临界点附近解析,则它可以被展开成关于序参量的多项式函数。然后体系真实的自由能对应于Landau自由能的极小值/稳定态。【注意这个内禀序参量的变化不能人为直接控制,只能通过间接调控外界压强和温度等间接控制。】
值得注意的是:因为我们假定体系具有反演不变性,所以这里的Landau自由能函数里没有关于序参量的三次方项。
首先考虑自发磁化,即当外场时Landau自由能函数的行为:
所以可以解出三个极值点,其中1个零解加上另外一对互为相反数的非零解(注意:取决于和的具体符号,因为在根号里面,这一对解在有些时候不一定存在):
我们希望找到稳定的极值点,也就是最小的地方作为系统可以稳定存在的状态。所以基于这个要求,首先必须让四次项前面的系数以保证当时不会变成负无穷大(那样的话系统的稳定态就要落在的地方以保证能量最低,这显然是不合理的)。由于,所以二次项前面的系数的正负直接决定了是否存在非零解。
当时,非零解根号里的宗量小于0,此时只存在的唯一解。为了知道的解对应的极小值(稳定态)还是极大值(非稳定态),我们看对序参量的二阶导数在处的符号,如果是正号就意味着这对应稳定态,否则就是非稳定态:
所以处对应能量的极小值,确实对应时的稳定态。为直观起见,作出此时的函数关系草图(【图9】类似一个“”型曲线):
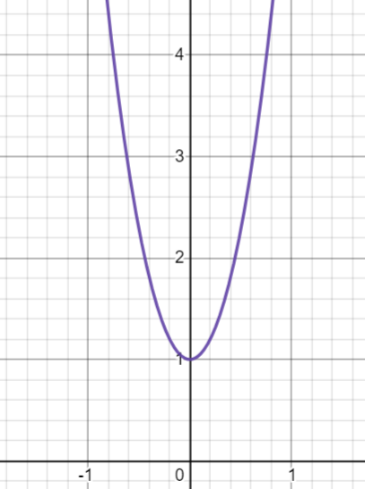
图9 - ,,纵坐标是自由能,横坐标是序参量。容易看出处对应该函数的极小值(稳定态),所以此时系统处于高温下的无序相(完全对称!)
从另一方面看,又代表高于相变临界温度时的无序相。所以我们以序参量 为桥梁找到一个对应关系,即:时。
当时,非零解根号里的宗量大于0,此时存在3个极值点,即最开始列出的:
为了知道这3个解对应的极小值(稳定态)还是极大值(非稳定态),我们看对序参量的二阶导数在这3处的符号,如果是正号就意味着对应稳定态,否则就是非稳定态:
所以处对应能量的极大值,是非稳定态。而处对应能量极小值,是稳定态。所以体系此时处于的稳定态。为直观起见,作出此时的函数关系草图(【图10】类似一个“”型曲线):
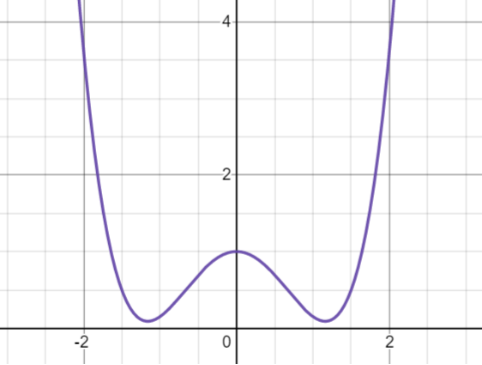
图10 - ,,纵坐标是自由能,横坐标是序参量。容易看出处对应该函数的极大值(非稳定态),处对应该函数的极小值(稳定态)。所以此时系统处于低温下的有序相(对称性破缺!)
从另一方面看,又代表低于相变临界温度时的有序相。所以我们以序参量为桥梁又找到一个对应关系,即:时 。
所以综上所述,我们找到了Landau自由能函数二次项前面的系数A和温度T在临界温度附近的关系,即:时;而时。
出于连续性的考虑可以推断出恰好在临界温度时。为直观起见,作出此时的函数关系草图(【图11】类似一个“”型曲线):
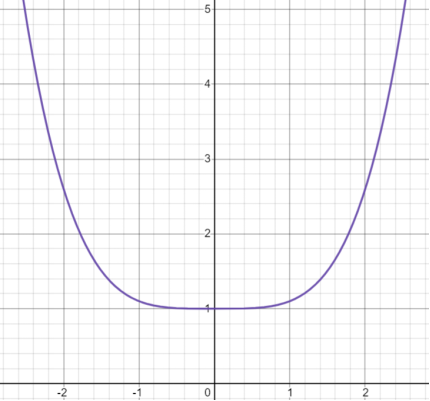
图11 -,,纵坐标是自由能,横坐标是序参量。容易看出处对应该函数的极小值(稳定态),但相较于图9,此处在极小值点附近有一个接近于平坦的谷底,对应于相变临界点处关联长度趋于无穷大。温度稍微提升一点图11就会进入图9的无序相,温度稍微下降一点就会进入图10的有序相
根据上述和温度的关系,可以把在处作泰勒展开到一阶:
其中。当从临界温度下方趋于临界点时,由于还在有序相,所以:
当从临界温度上方趋于临界点时,由于在无序相,所以。所以当从临界温度下方趋于临界点时,序参量是以的方式趋于0的;当从临界温度上方趋于临界点时,序参量恒为0。所以我们得出Landau二级相变理论里序参量的临界指数是1/2!这个结果和之前气液相变里序参量(密度差)的临界指数以及平均场近似下Ising模型里序参量(平均自发磁化)的临界指数完全一样!
下面看Landau二级相变理论里磁化率的临界行为。磁化率的计算牵涉到磁场的变化。所以我们必须使用带有磁场的Landau自由能展开。这个附加的磁场是通过与序参量(这里的可以解释成磁矩)一次方形式的耦合进入到Landau自由能的,即:
【注意如果我们处理的不是磁性体系和磁化率,而是希望用Landau自由能描述气液相变里压缩系数的临界行为的话,只需要把这里的序参量解释成密度差(或体积差),外场解释成压强即可。】
在系统稳定态处Landau自由能取极值:
所以体系磁化率是:
当从临界温度下方趋于临界点时,由于还在有序相,且磁场为0,所以,代入到上面关于的表达式得到:
当从临界温度上方趋于临界点时,由于在无序相,且磁场为0,所以,代入到上面关于的表达式得到:
所以我们发现不管是从临界温度下方还是上方趋于临界点,磁化率都是以的方式趋于无穷大(发散)的!所以我们得出Landau二级相变理论里磁化率的临界指数是1!这个结果和之前气液相变里等温压缩率的临界指数以及平均场近似下Ising模型里等温磁化率的临界指数完全一样!
下面再看Landau二级相变理论里比热的临界行为。在比热的讨论里和外磁场没关系,所以。所以Landau自由能的形式退化成:
体系的化学势(吉布斯自由能)取在Landau自由能的极小值(稳定态)处。所以在临界温度以下()时,体系的化学势取在Landau自由能的地方,即:
在临界温度以上()时,体系的化学势取在Landau自由能的地方,即:
所以临界温度以下()时体系的熵是:
临界温度以上()时体系的熵是:
所以可以进一步求出从临界温度下方趋于临界点时体系的比热是:
从临界温度上方趋于临界点时体系的比热是:
所以我们发现不管是从临界温度下方还是上方趋于临界点,比热都是以的方式发生奇异性(间断点)的!所以我们得出Landau二级相变理论里比热的临界指数是0!这个结果和之前气液相变里等容比热的临界指数以及平均场近似下Ising模型里比热的临界指数完全一样!
最后看固定在临界温度上,当外磁场很弱的情况下,和的关系。此时二次项前面的系数,并且因为接下来的计算牵涉到磁场的变化,所以我们必须使用带有磁场的Landau自由能展开。这个附加的磁场是通过与序参量 (这里的可以解释成磁矩)一次方形式的耦合进入到Landau自由能的。所以Landau自由能的形式是:
在系统稳定态处Landau自由能取极值:
所以固定在临界温度时(且外场很小时),磁场和序参量间满足三次方的关系:。这里的临界指数3也是标定Landau二级相变理论的一个特征指标!这个结果和之前气液相变里偏离压强和体积临界值的小量间满足的关系所对应的临界指数3,即,以及平均场近似下Ising模型里的磁场和平均磁化或平均磁矩间满足的关系所对应的临界指数3,即或,完全一样!
4对称性和普适类
所以从上面的分析中我们发现在临界点附近:气液相变,平均场近似下的Ising模型,和更为抽象一般的Landau二级相变理论都给出了完全相同的一组临界指数!看起来相互间没有任何关系的体系(气液相变,Ising铁磁相变体系,和Landau二级相变理论所描述的更为抽象一般的体系),出发点和处理手法也完全不同(气液相变里是从非理想气体所满足的物态方程出发,Ising铁磁相变体系是从平均磁化满足的自洽方程出发,Landau二级相变理论是从作为序参量的多项式函数的Landau自由能出发),竟然在临界点附近的行为表现出惊人的一致性!!!
这种一致性产生的根本原因在于:气液连续相变,Ising铁磁相变体系,和Landau二级相变所描述的更为抽象的体系具有完全相同的对称性,即所谓的对称性!所以它们所描述的体系处于完全相同的普适类里!如果把普适类看成是一类几何/拓扑对象,那么这些临界指数就可以看成是标定这个几何/拓扑对象特征的“拓扑不变量”!这些“拓扑不变量”和具体物质(可以类比成对象局域的几何性质)无关,而只与体系的对称性(可以类比成对象本身的拓扑性质,比如亏格和缠绕数)有关,具有普适性。
然而值得注意的是,这个普适性也是有限度的。比如这三套理论对于比热临界指数的估计都是0(这与实验中测出的非零的比热临界指数差别很大),这是因为它们完全忽略掉了体系本身的热涨落效应,所以它们只能给出一种特殊的普适类。对于具有别的对称性的体系(比如二维XY模型),它将属于别的普适类。别的普适类将由别的一组临界指数标定。
所以自然界中千差万别的体系可以被划分进不同的普适类里,每个普适类内部的所有系统在临界点附近都是完全等价的,所以只要研究清楚普适类里其中一个系统在临界点处的行为,我们就可以直接推断出别的和它在同一个普适类里的其它系统在临界点处的行为!所以对不同的具体系统的物理性质的研究可以转化为对不同普适类的抽象数学性质的研究!而这也是相变和临界现象问题里最引人入胜的地方之一。
 最前沿的电子设计资讯
最前沿的电子设计资讯