
本文示例的是较为常见的一阶RC积分电路,从时域角度来说,大家可能都听过RC时间常数,那么其充放电过程是怎样的?频域特性如何?有何规律,笔者借此篇文章和大家一起简单了解下,本文使用Sigrity Topology Explorer 17.4仿真软件。
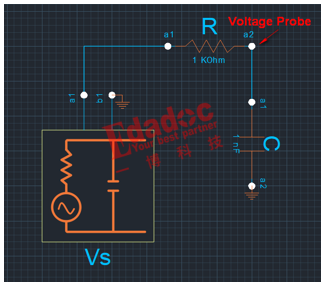
先搭建一个简单的电路模型,观察时域波形,1V恒压源,路径上使用RC串联电路,R值为1Kohm,C值为1nf。探测电容端的充电电压及电流,仿真结果如下:
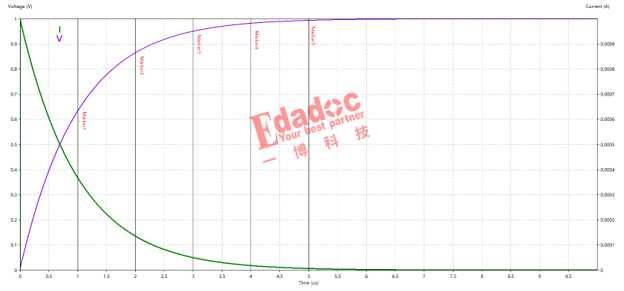
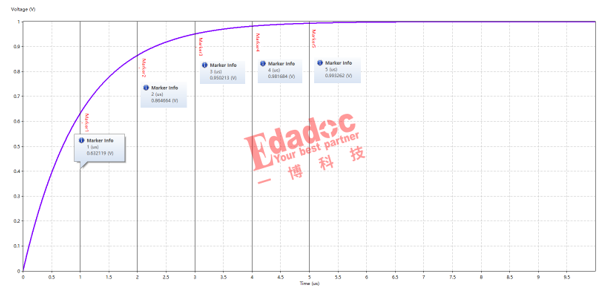
通过时域结果可以看到电容两端的电压和电流的变化,第二张图是标记了不同时间常数下的电容电压值。
电源V通过电阻给电容C充电,V0为电容上的初始电压,Vc为电容充满电后的电压,Vt为t时刻的电容电压,便可以得到以下计算公式:
Vt=V0+(Vc-V0)*[1-e^(-t/RC)],其中时间常数T=RC
在此链路中T=1*10^(-9) F * 1*10^3 ohm =1us,所以1T=1us。
每经过一个时间常数,电容两端的电压上升(1-1/e)大约是电源电压和电容两端电压之差的63.2%。从电路接通电源开始:
1us时,Vt=0+(1-0)*(1-1/e)≈0.632V,
2us时,Vt=0.632+(1-0.632)*(1-1/e)≈0.865V,
3us时,Vt=……
4us时,Vt=……
5us时,Vt=……
……
理论上5个时间常数后,电容基本上接近充满的状态了,不过是不可能完全充满的,因为公式里面的指数函数的值不可能会等于0,随着时间的无限延长,电容两端的电压也会无限趋近于1v,和前面仿真看到的时域响应的波形吻合。
了解时域的响应后接着看下频域响应,画出对应的电路图:
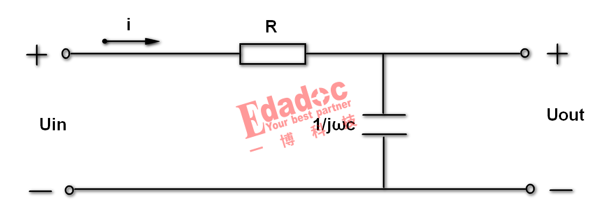
由频域模型图得知电阻的比值,即可计算出电路的网络函数表达式:H(ω)=Uout/Uin=1/(1+jωRC)
幅频特性大致如下图:
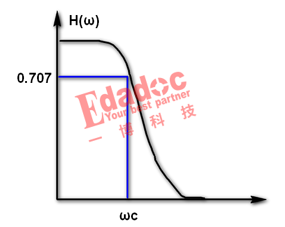
可以看到,低频输出幅度大,高频输出幅度小。选择适当的截止频率可以让信号的有效成分通过且使其夹带的毛刺得到合理抑制,这里的放大倍数0.707实际上也是我们常提到的增益为-3db的点,表示输出占输入幅度的1/ωc=1/RC也作为截止频率衡量滤波性能的定性指标。由于具备这种频域特性,这种RC积分电路常被用作于滤除高频的一些毛刺噪声。
好了,这期关于RC电路的分享就到这里,还有更多内容读者们敬请期待。
 最前沿的电子设计资讯
最前沿的电子设计资讯