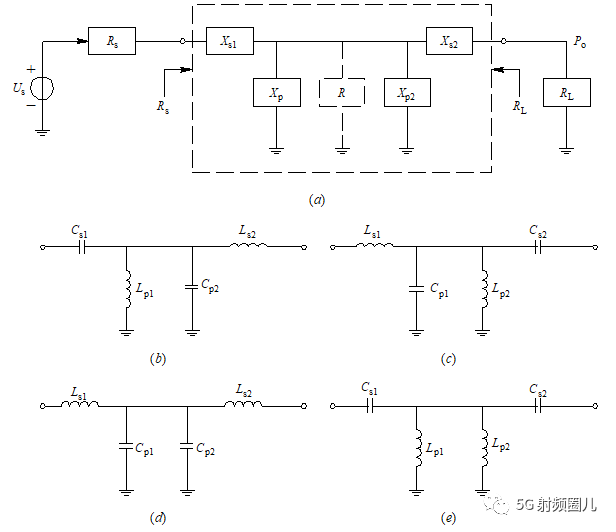
T型匹配电路的分析方法可参照L型匹配电路，我们不再详细说明，其计算公式如下： 
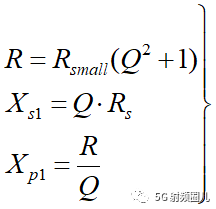
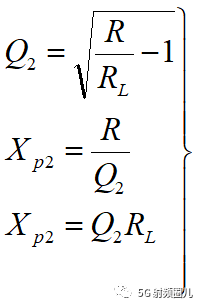
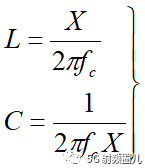4.1.3 Π型匹配电路 Π型匹配电路的结构如下图a所示，我们这里只根除设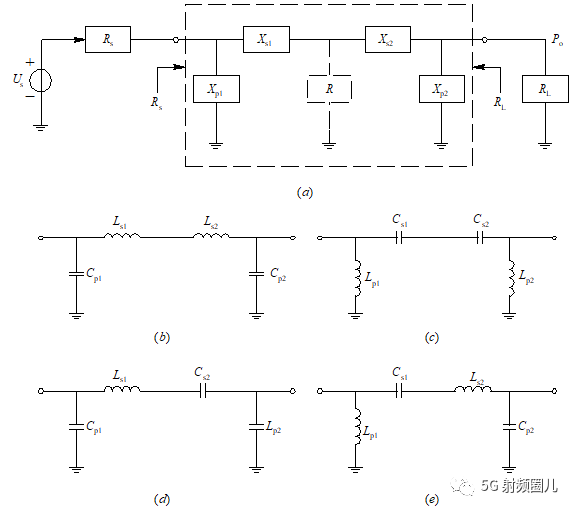计公式。 
设计公式：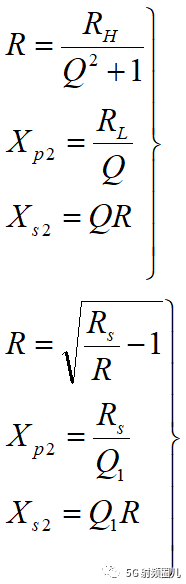 
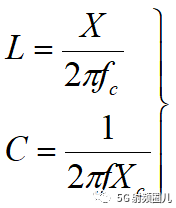对于电路匹配，有一个重要的工具，就是史密斯圆图，现在很多的射频电路仿真软件上，如ADS和AWR等，都集成有史密斯圆图工具，我们可以利用史密斯圆图，快速得到电路的匹配网络。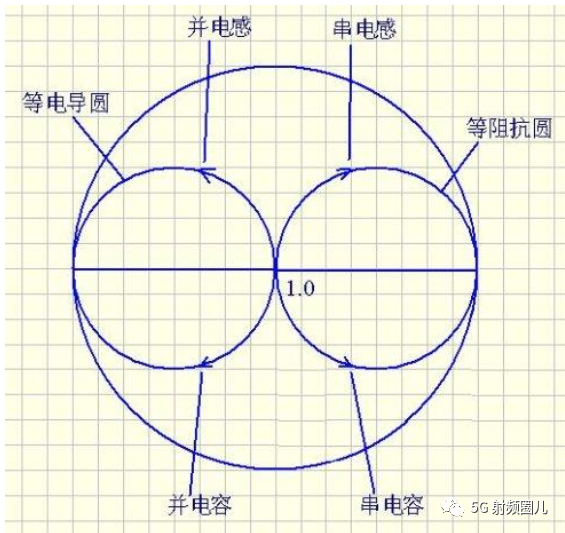 
No4.2 Smith Chart 匹配示例 问题： 设计一个L型匹配网络，使其在频率500MHz处，完成负载到传输线的匹配。负载阻抗为ZL=200-j100Ω，传输线阻抗为Z0=100Ω。 这个问题的示意图如下：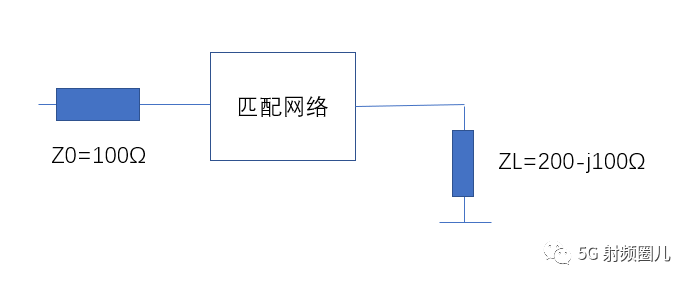 
常见的L型匹配电路有两种，左L和右L，具体选择哪种，可根据源阻抗与负载阻抗的大小关系来定S(不得不掌握的几种常见的集总参数阻抗匹配电路)。 
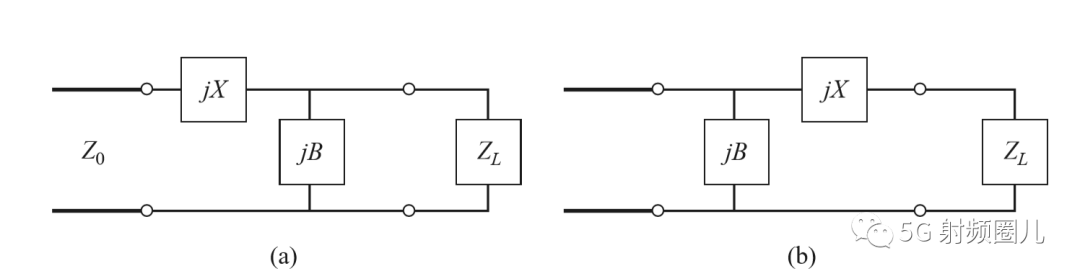首先我们将负载阻抗ZL归一化得到zL=2-j，把这个点标注在Smith 圆图上。这个点在1+jx的圆内部，所以我们选用右L型匹配电路，或者按照我们上节学习到的规律RL>RS(不得不掌握的几种常见的集总参数阻抗匹配电路)。从负载看过去，第一个元件时并联电纳B，通过负载话SWR圆，且从负载过圆心画一条直线，就可以把负载阻抗转换成导纳，才能与该并联导纳相加。 我们加上这个并联导纳之后再转换回阻抗，将它画在1+jx圆上，这样我们才能加上一个串联电抗来抵消jx并与负载匹配。也就是说，这个并联电纳B能够将YL转移到Smith圆图的1+jx圆上。我们可以看到在外加一个jb=j0.3电纳之后，便能沿着等电导圆移动到y=0.4+j0.5处，再将导纳转换成相应的阻抗z=1-j1.2，在此处接上串联电抗x=j1.2就可实现匹配。使我们回到Smith圆图的中心点。 详细过程如下： 
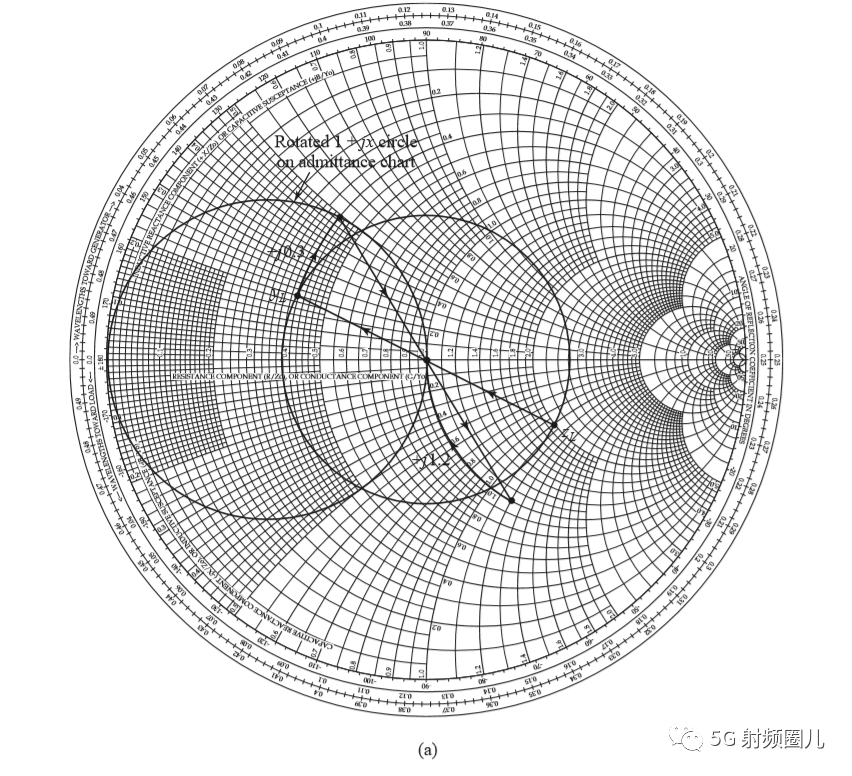如果该匹配电路是由一个并联电容和串联电感组成，如下图所示，在频率f=500MHz处，可求出该匹配电路的电容值和电感值。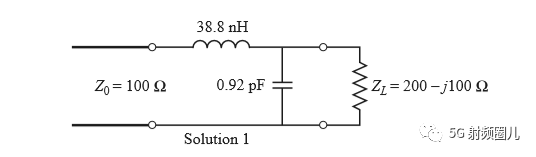 
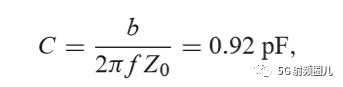
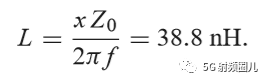如果我们用一个b=-j0.7的并联电纳来替换之前外加的b=j0.3的并联电纳，则在移位后的1+jx圆的下班圆移动这个点到y=0.4-j0.5处，然后转换回阻抗并且加上一个x=-1，2 的串联电抗，也可以达到匹配。这时，匹配网络使一个有并联电感和串联电容来实现。在频率f=500MHz时的电感和电容值可以计算得出：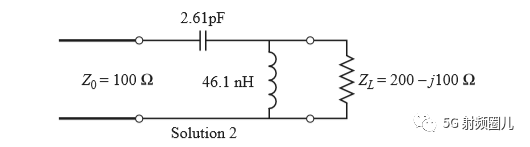 
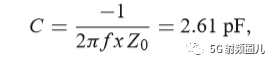
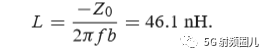对于这两种匹配网络，其反射系数的大小与频率的关系如下图所示。 
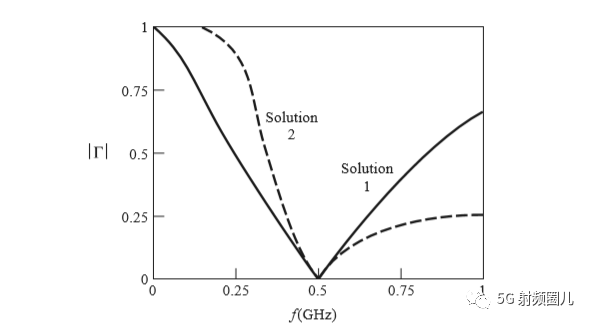如果单纯从匹配角度来说，两种方案都可以选择，匹配带宽没有明显的区别。但是实际应用中，可以根据射频电路的需求进行选择。比如是否需要隔直？是否需要滤波？实际电感和电容的选型等等。 No4.3 短截线匹配法 用集总参数元器件进行阻抗匹配，大家理解起来比较容易，但是在微波电路中，我们常常不喜欢加进去那些林林总总的电感电容，一个原因是贵，另一个原因则是对应值的电感电容很难取寻找。我们通常希望直接在线上进行匹配。今天，我们一起来看一下如何利用一段传输线来进行阻抗匹配？ 
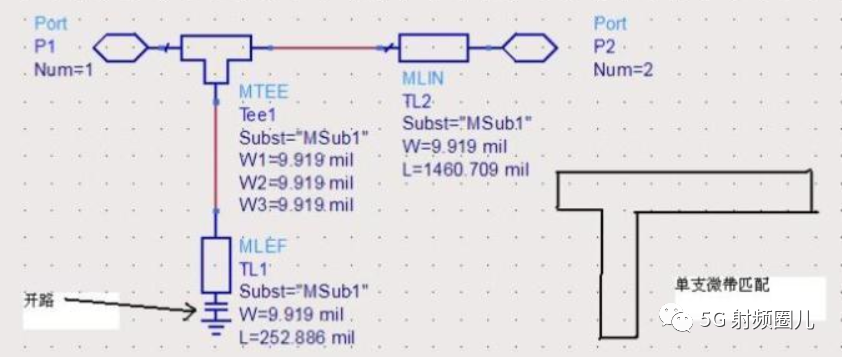最常用到的短截线匹配法有单支节和双支节，有双支节了，当然还会有多支节。我们就最常用的单支节和双支节进行讨论。 
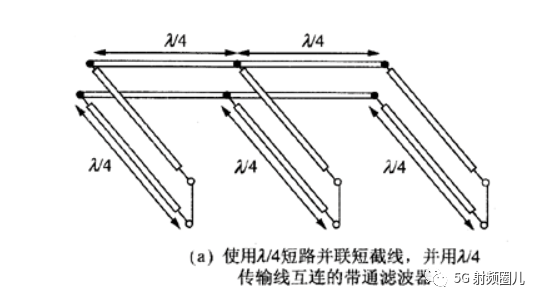单支节就是使用单个开路或者短路的传输线段在距离负载某一确定位置处，通过与传输线的并联或者串联，实现阻抗匹配。如下图所示。在这种单支节短截线匹配电路中，有两个可调节的参数，第一个是从负载到短截线的距离d，第二个就是短截线所能提供的电纳或者电抗，短截线所能提供的电纳或者电抗实际上是由短截线本身的特性阻抗Z0和短截线的长度决定。因此，单支节短截线匹配法实际上是对短截线到负载距离d和短截线特性阻抗Z0，以及短截线长度L这三个参数组合优化。 
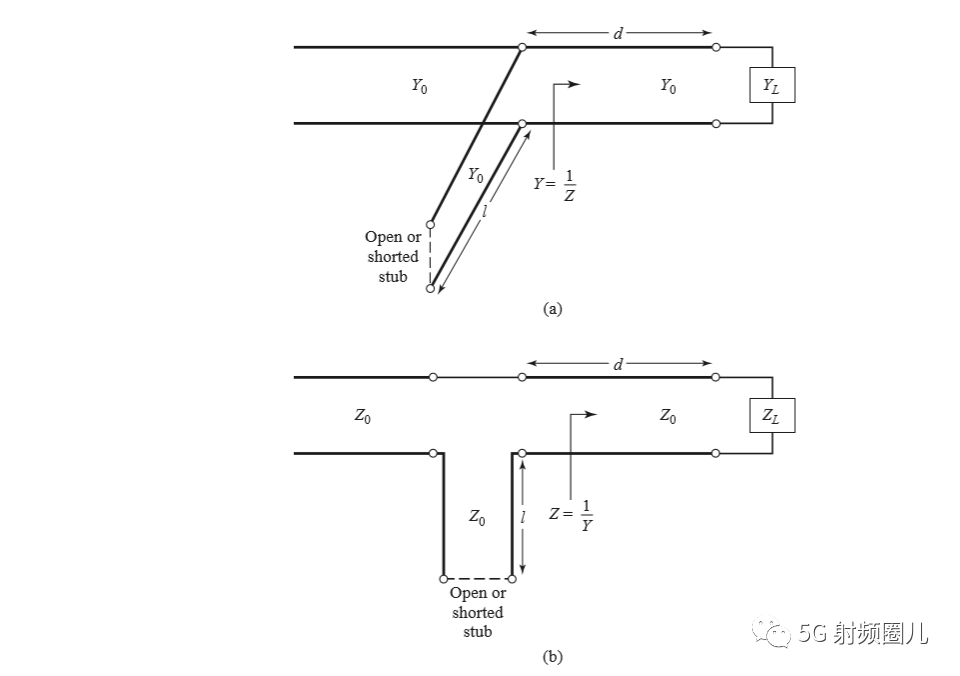对于并联短截线，其基本思路是首先确定短截线到负载的距离d，在此点向传输线方向看过去的导纳为：Y=Y0+jB，然后选择短截线的电纳为-jB，就可以达到匹配条件。 对于串联短截线，短截线到负载的距离d，在此位置，向传输线方向看过去的阻抗为Z=Z0+jX，那么选择短截线的电抗为-jX，便达到阻抗匹配的条件。 另一个就是双短截线匹配。双短截线匹配，增加了设计参量，提高了设计的灵活度。双短截线匹配电路如下图所示，负载到第一个短截线的距离不再有特殊要求，但是两个短截线直接的距离d是有要求的。 
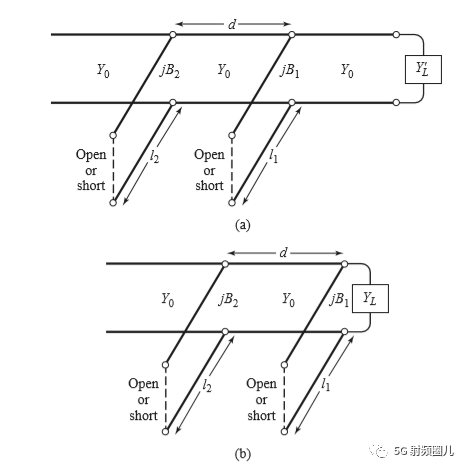在《微波工程》中，作者通过两个例子，利用Smith圆图对单路短截线的参数进行求解。具体过程，请参照书籍。推荐在设计中，利用仿真软件进行匹配，因此，理论推导过程不再赘述。 No4.4 四分之一波长阻抗变换器 常用的阻抗匹配方法很多，我们今天一起来学习下四分之一阻抗变换器匹配的原理。 
四分之一波长阻抗变换器是有一段长度为lambda0/4，阻抗为Z01的传输线构成，其中Lambda0是传输线所传输信号的中心频率所对应的相波长，与信号频率f0，传输线的结构，填充介质等因素有关。当传输线的终端接纯电阻负载RL时，在中心频率上的输入阻抗为：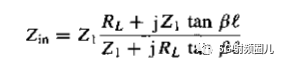 
为了计算该式在
时的值，我们可以用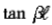
去除上式的分子分母，并取
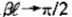的极限，即可得： 
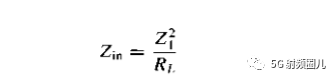为了使反射系数等于0，必须有Z0=Zin，可得四分之一波长变换器的特性阻抗为： 
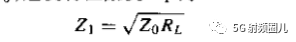可以看出了，这个阻抗就是负载阻抗和传输线阻抗的几何平均。因此在传输线上就没有驻波，反射系数为0，但是在四分之一阻抗变换器内还是有驻波存在。变换器上的驻波系数为： 
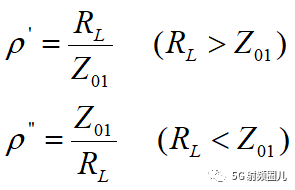注意：上式是基于信号的中心频率f0来求解的，因此只能在这个点上实现匹配，或者匹配线的长度是该频率的四分之一波长或者四分之一波长的奇数倍（2n+1）处实现完全匹配，在其他频率上将会失配。 上式只能用于实阻抗匹配，即负载的阻抗为纯电阻。但是对于一般的复阻抗负载，ZL=RL+jXL，时，一般先经过一个适当长度的传输线把负载阻抗变换为实阻抗负载。下面介绍两种常用的匹配方法：
方法一：终端接四分之一波长阻抗变换器的同时，并联一段特性阻抗为Z0，长度为s的终端段路线。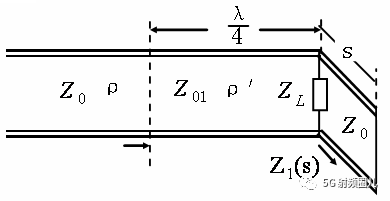 
终端短路线在负载处提供一个纯电抗，只要选择合适的长度s，就可以使其在负载处所呈现的电抗来抵消负载的电抗部分，从而使负载的总阻抗为实数，然后利用四分之一波长阻抗变换器将负载处的等效阻抗变换为Z0，实现阻抗匹配。
方法二：在靠近终端的电压波腹点或者波节点处接入四分之一波长阻抗变换器来实现复阻抗匹配。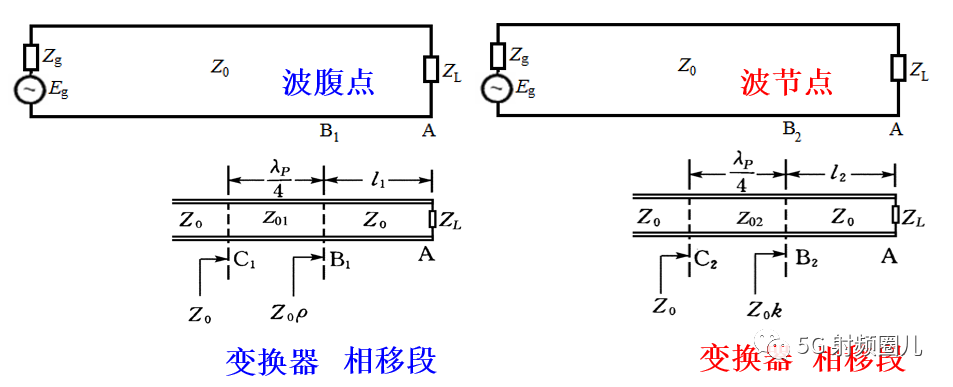 
传输线上电压波节点或者波腹点的阻抗为实数，所以如果在这两个位置剪短传输线，接入特性阻抗为Z01的四分之一波长变换器就可以进行阻抗匹配。负载与电压波节点或者波腹点位置的传输线称为相移段。
1，当电压波腹点接入四分之一波长变换器时，相移段长度L和变换器特性阻抗分别为：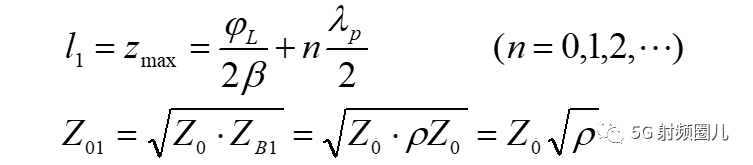 
2，当电压波节点接入四分之一波长变换器时，相移段长度L和变换器特性阻抗分别为： 
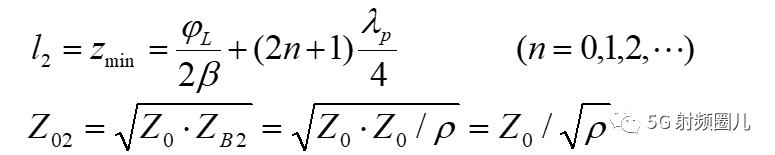这个时候阻抗变换器上的驻波系数为： 
为了更深入的了解四分之一波长阻抗变换器的特性，我们一起来看一下多次反射的概念。 
对于上图给出的四分之一波长变换器，它具有一下的反射系数： 
这些反射系数可以表示为：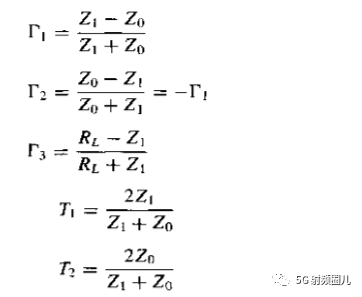 
我们可以想象一下，当电磁波信号沿着传输线进入四分之一波长变换器时，它首先看到的阻抗是Z1，因为还没有到达负载RL，因而负载还看不到它的影响。一部分电磁波被反射，另一部分被传输进入四分之一波长变换器，然后被传输的电磁波到达负载时遇到了组在阻抗RL，再次被反射，经过四分之一波长到达传输线和变换器的交界处，遇到阻抗Z0，再次被反射回到负载，电磁波在变换器内不断额被反射吸收，每次反射波都要经过往返两次四分之一波长，产生相位差180°，总的反射系数就是这无数次反射系数的和： 
经过一系列的计算： 
我们发现，当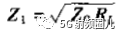
时，上式为0，那么总的反射系数也为0，传输线是匹配的。
那么我们发现四分之一波长变换器匹配的原理就是通过选择恰当的匹配段的特性阻抗，和长度，使得所有的部分反射的结果叠加为0，来消除组播，形成整个传输线上的行波。可见变换器内部的斗争还是蛮激烈的。 小结：其实到这里，阻抗匹配还远远没有结束。在很多的射频电路中，宽带阻抗匹配才更利于整个系统设计。但是最为高级的一个阻抗匹配方式就是滤波器的设计。让我们在以后的章节慢慢完善阻抗匹配吧。
最前沿的电子设计资讯
