
在进入正文之前,我们首先来看一段故事,在1666年,牛顿曾经观察到了这样一个现象,当一束阳光照射在棱镜上的时候,他观察到从棱镜中出来的光分成了各种不同的颜色。

图源 Wikipedia
当时,大多数科学家都认为白光是一种单一颜色的光。这一发现则纠正了当时科学家的这个固有观念,让后世的人们认识到,白光其实是由各种不同颜色的光混合形成的。

1
电磁波

麦克斯韦方程组归纳了电磁学的主要成果,并且预言了电磁波的存在,并且确认了光本质上是电磁波。描述电磁波,或者任何波动,都离不开两个量:频率和相位。
电磁波是什么呢,电磁波其实就是电磁场随空间和时间的周期性振荡。在数学上,电磁波是麦克斯韦方程组的解。选择不同的边界条件,人们可以得到不同形式的解,平面波是一种形式简单的解,我们就来讨论平面波。

图源 pixabay
平面波其实就是正弦和余弦函数,在欧拉公式的帮助下,也可以用指数函数来描述。这和我们日常生活的印象是一致的,波动就是某个量随着时间和空间的周期性变化,而正弦和余弦函数就是随着它们的自变量周期性变化的。
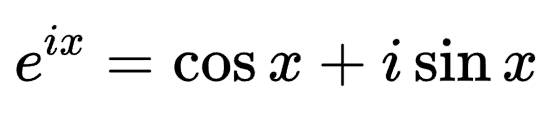
欧拉公式将指数函数和三角函数联系起来
为了使公式变得简单,人们更多地使用指数函数,因为指数函数的乘除可以直接转化成自变量的加减,而如果使用三角函数则需要背诵复杂的和差化积公式。
从麦克斯韦方程组获得平面波形式的解需要引入两个重要的参数,它们分别是频率ω和波矢k,其中频率ω描述的是时间的周期性变化,而波矢k描述的是空间的周期性变化,二者之间由光速相互联系。
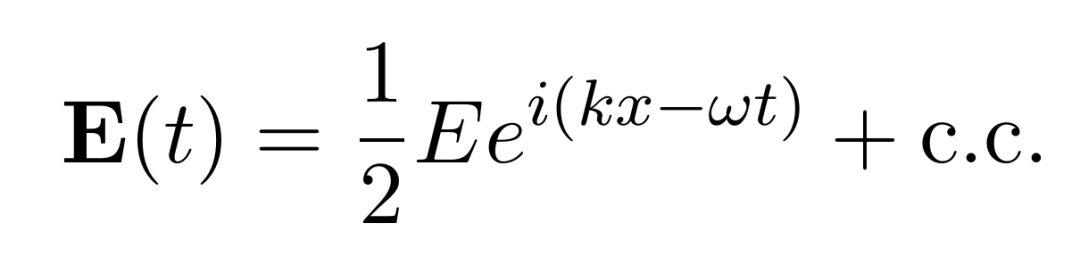
现在我们已经引入了频率作为描述电磁波随时间变化快慢的参数,它是指单位时间内通过空间中特定点的波的周期数。在波动光学领域,频率通常以赫兹 (Hz)为单位进行度量。光的频率对应着它在可见光谱中的颜色。较高的频率对应于较短的波长,在真空中,光速恒定,光的频率与其波长成反比。而量子力学认为单个光子的能量正比于该光子的频率,因此频率越高的光,单个光子的能量越高。
而另一个参数,相位,则描述某一状态处于周期性变化中的什么位置。相位是一个像角度一样的量,周期性运动就像转圈,我们可以用某个状态对应的圆心角来确定这个状态在一个周期内的相对位置,所以我们常用弧度作为相位的单位,每完成一个周期相位就增加2π,或者相位就归零一次。

2
干涉

干涉是波动光学的重要话题,是指两个或多个相干光波重叠,导致光束交叠区域的光强不等于两束光各自强度的加和,而是形成明显的亮区和暗区图案的现象。这种现象是由于光波电磁场的叠加而产生的。
当两个相干光波相遇时,它们的电场和磁场在空间的每个点处叠加在一起。如果波峰重合(相位相差π的偶数倍),它们就会相互增强,从而产生相长干涉和更高的光强。相反,如果一个波的波峰与另一波的波谷对齐(相位相差π的奇数倍),它们就会相互抵消,导致相消干涉和较低的光强。
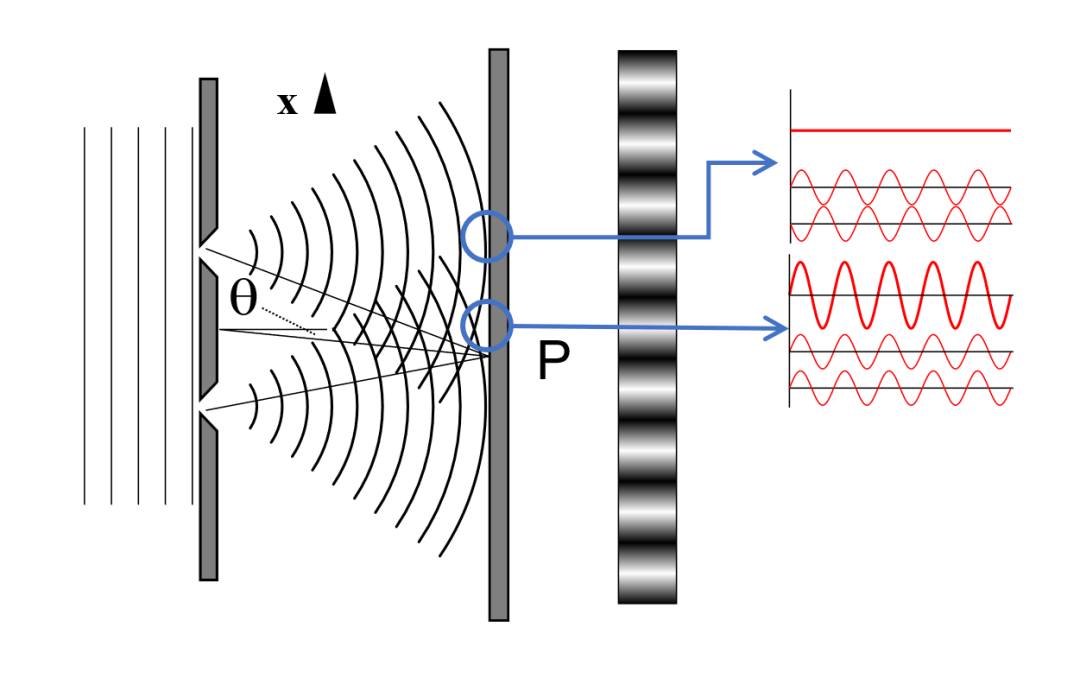
我们观察到的光强其实是电场强度的模平方并且对时间取平均值。电场强度的模平方存在不恒为零的交叉项,就是下图中的cos项,这一交叉项与相两束光的相位差有关。随着相位差的不同,我们可以观察到光强的空间分布情况。
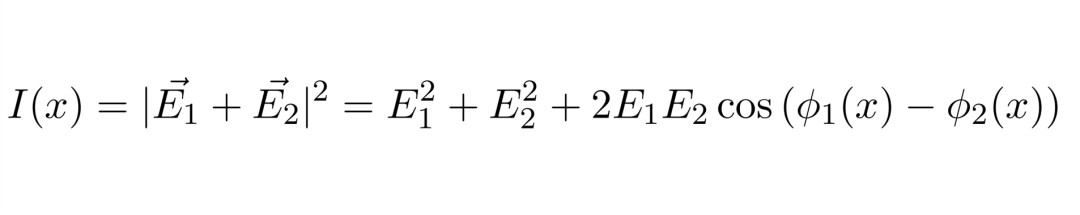
只有交叉项不为零才会出现干涉现象,如果两束光的频率相等,并且相位差恒定,那么交叉项一定不恒为零。
光的频率决定了干涉条纹之间的间距。较高频率的光(较短波长)产生的条纹靠得更近,而较低频率的光(较长的波长)产生的条纹间隔较远。当含有不同频率的波干涉时,它们可以产生复杂的图案,因为相长干涉和相消干涉不仅取决于相位,还取决于频率。不同频率的波产生的亮条纹出现在不同的位置。

图源 Wikipedia

3
脉冲

实际存在的光源不可能发出在时间和空间上无限延续的平面波,它们发出的光一定是有限时间长度的波包。
波包是什么呢?波包就是大量不同频率的光叠加形成的波,也称为脉冲。
如果有几个不同频率的波叠加起来会发生什么,我们来看下面这张图。
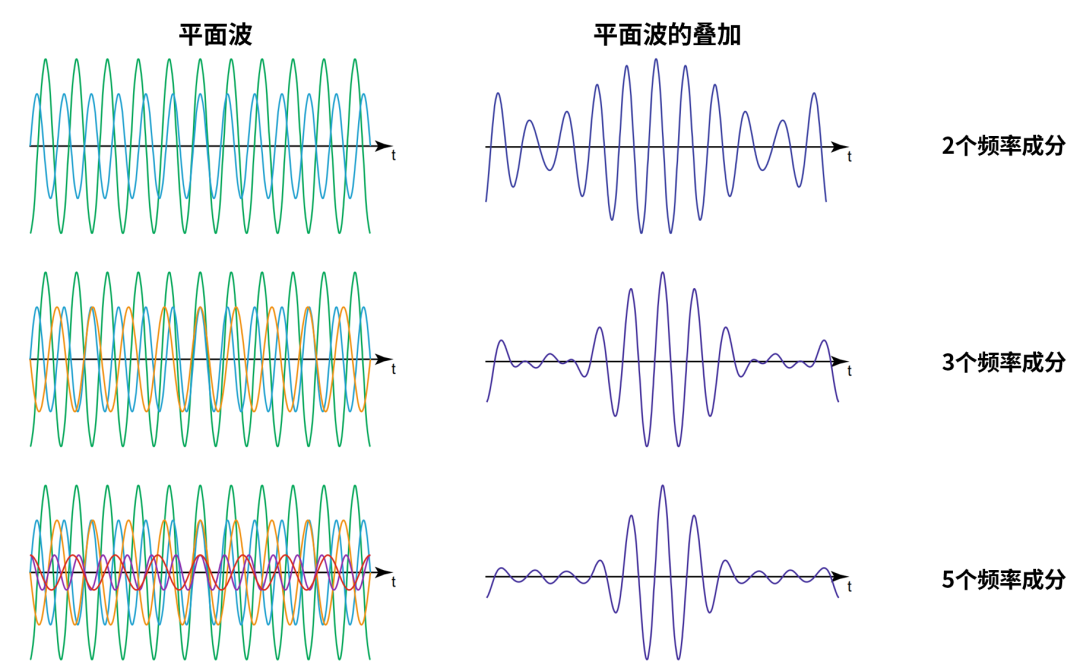
图源[1]
这张图显示了不同离散频率的平面波在空间固定位置的叠加可以形成波包,也就是光脉冲的原理。随着叠加中使用更多频率分量,远离脉冲最大值处的振幅明显下降。
这里是具有恒定频率间隔的平面波叠加的示例,并且由于参与叠加的频率是离散值,最终的叠加结果不仅仅是一个脉冲,而是一个周期性脉冲串。相反,如果频率是连续的则仅产生一个脉冲。另外参与叠加的频率范围越大,得到的脉冲就越短。
对于传统光源来说,受激原子/分子在从激发态跃迁到基态时会发光。然而,激发态的寿命是有限的。这里所说的寿命是说分子中电子处于激发态的时间,经典物理的图像是偶极子保持激发并进行振荡的时间。对于持续有限寿命而不是无限时间激发偶极子,发射的光也就是持续有限时间的波包。
因为激发态有着有限的寿命,激发态和基态之间的能量差存在不确定度,跃迁时发光的频率也就存在不确定度,这一范围内的频率叠加产生长度有限的脉冲。
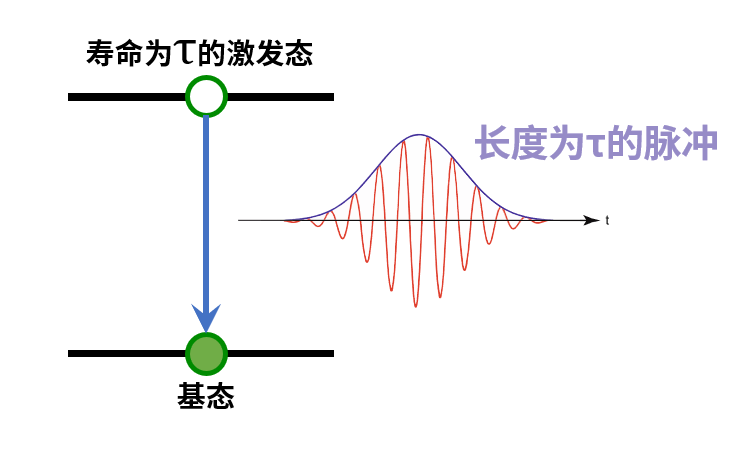
还记得我们一开始提到,白光是各种不同频率的光混合形成的。那么我们是不是可以认为白光一定是非常短的脉冲呢?其实不一定。
我们前面讨论不同频率的平面波叠加时假定了各个分量存在确定的相位关系:那就是它们都有一个波峰是重合的。如果这个相位关系不满足了会怎么样呢?
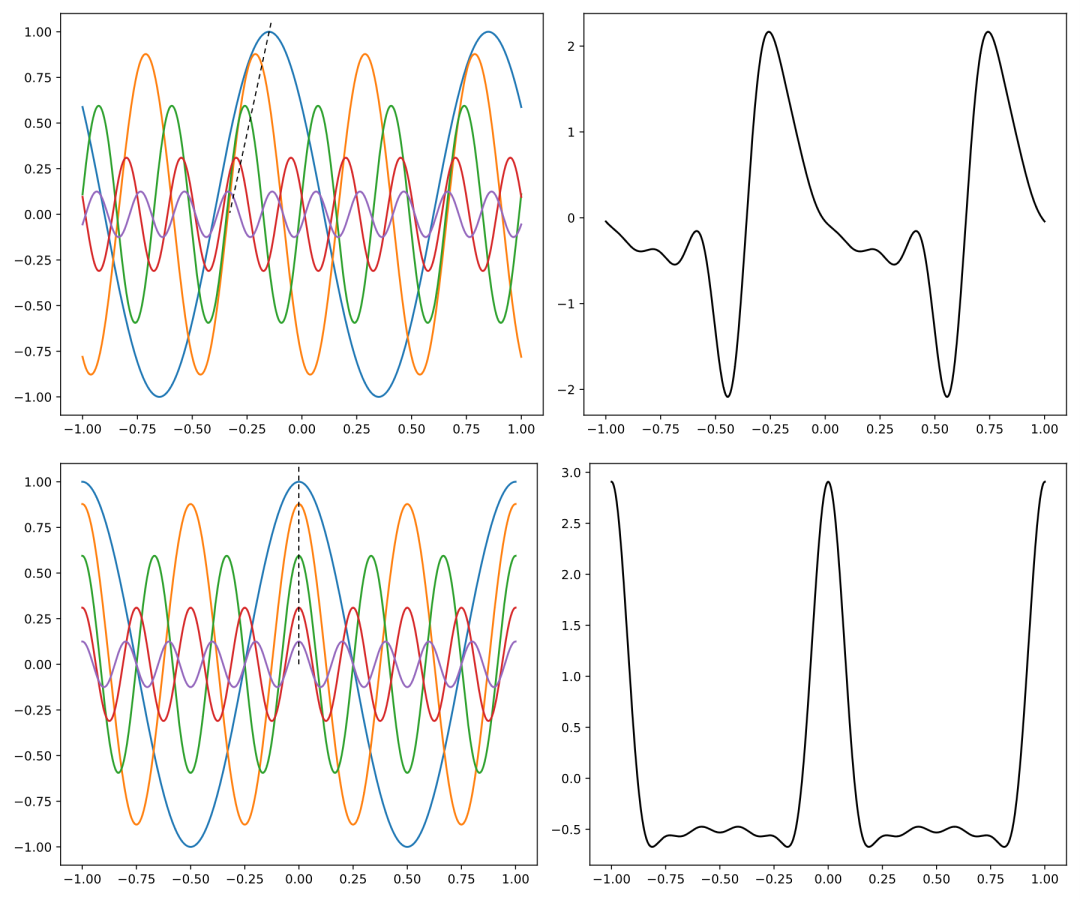
比如上面这张图里,上面那一行每个频率分量都相对下面那一行发生了一定的相位移动,可以看到波形相对于下面一行变得更宽了。这种现象我们称之为啁啾。通过下面这张图可以更形象地看到啁啾带来的影响。
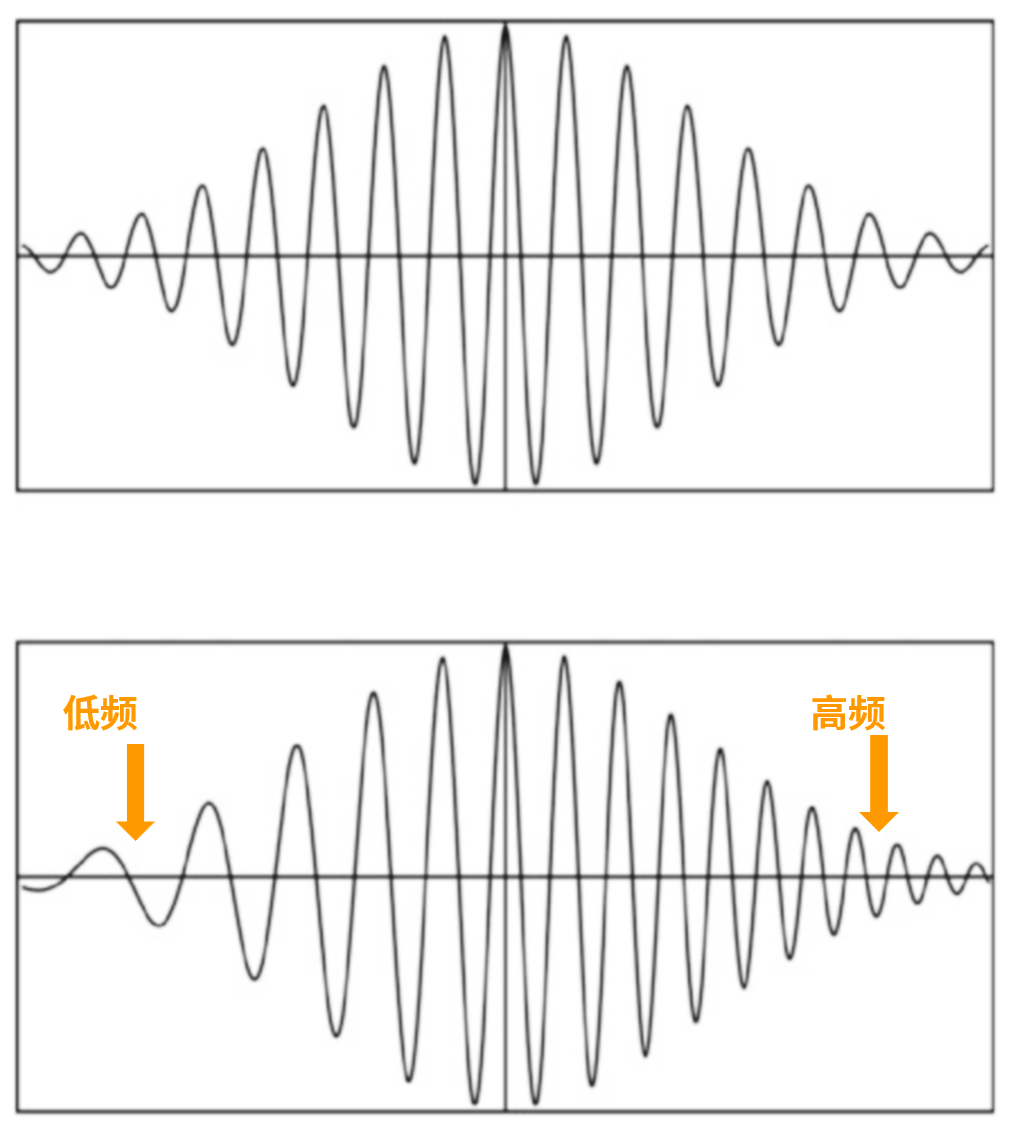
图源[1]
图中上半部分的波包是没有啁啾的高斯波包,下面的是引入啁啾的高斯波包,我们可以看到,下面这张图中高频的成分出现在更靠右的位置,而低频的成分出现在更靠左边的地方。
存在啁啾的波包不同颜色的成分部分地相互分开,会使波包整体变得更宽。另外,如果不同颜色的波分开得足够远,它们相互叠加的程度会很低,但是对于探测器来说,这些频率成分分离得并不远,探测到的仍然是白光。这时的白光虽然是大量频率成分合成的,但并不是非常短的脉冲。

图源 pixabay

4
非线性

上面我们已经知道了频率和相位对于光的传播扮演了什么角色,但是新的应用在哪里?非线性光学就是一个新的应用。
物理学家们一直在想,能不能对波的频率进行操作。
图源 pixabay
频率对于单色平面波来说是一种固有属性,是不会随着波的传播出现变化的。但是当光进入物质时会与物质发生相互作用,利用这些相互作用人们可以对光的频率进行操作,例如把两束光的相加或者相减、例如产生更多的频率成分等,这都得益于晶体的非线性效应。
光作为振荡的电磁场进入晶体时,会引发晶体内部的带电粒子跟着运动,形成极化。极化对电场的影响不是线性的,与电场的平方、立方甚至更高幂次都有关系:
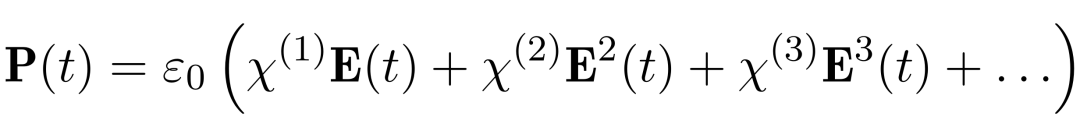
当光足够强的时候,这些高阶项带来的非线性效应才会表现出来。而常见的光源中,只有激光具有足够高的强度。
激光出现以来,利用非线性晶体对激光进行倍频、和频、差频的非线性光学也就发展起来。让我们来看一看这是怎么实现的。
如果两个频率的电磁波同时进入晶体,那么晶体中的电场就可以表示为
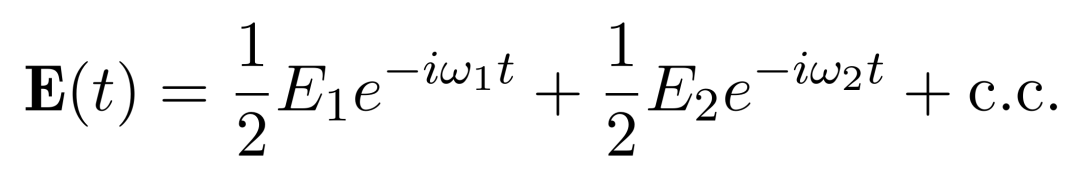
于是极化强度就可以表示为
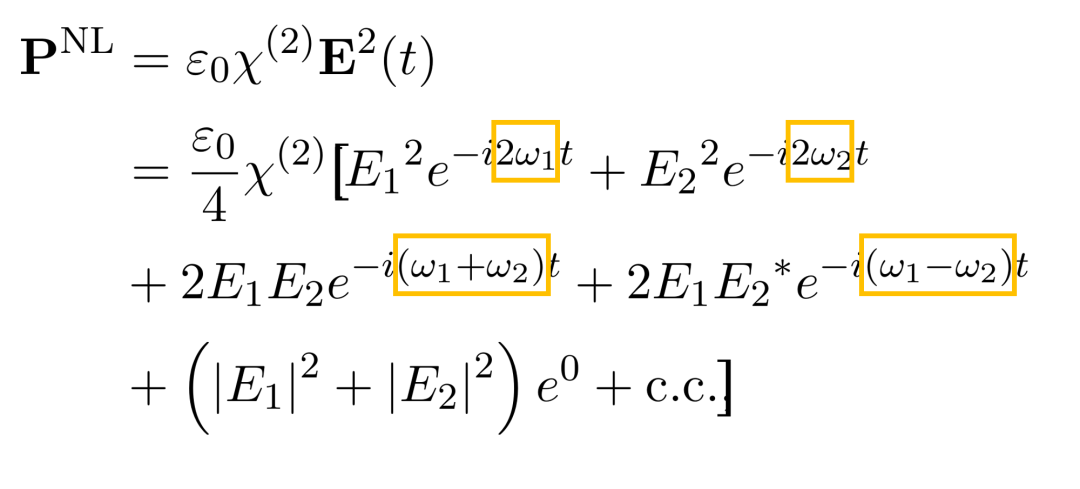
我们可以看到极化强度中有倍频、和频、差频的振荡出现,代表以这些频率振荡的偶极子的存在,这些偶极子将辐射出相应频率的电磁波,于是我们就得到了相应频率的光。

图源 pixabay
总之,我们首先探索光的频率和相位作为基本参数,它们支撑着我们对光的波动性的理解。进一步深入研究非线性光学,我们发现了光的行为超越线性传播的领域,并导致了和频产生等现象。 随着我们不断揭开光的奥秘,我们踏上了探索之旅,在迷人的光学世界中带来新的见解和无限的可能性。
参考资料
[1]Keller, Ursula, and R. Paschotta. Ultrafast lasers. Springer International Publishing, 2021.
[2]HECHT E. Optics[M]. Pearson Education, Incorporated,2017.
[3]Rulliere, Claude. Femtosecond laser pulses. New York: Springer Science+ Business Media, Incorporated, 2005.
 最前沿的电子设计资讯
最前沿的电子设计资讯